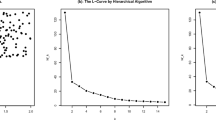
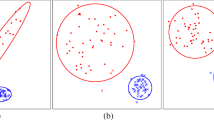
Abstract
In the cluster analysis, to determine the unknown number of clusters we use a criterion based on a classical location test statistic, Hotelling’s T 2. At each clustering level, its theoretical threshold is studied in view of its statistical distribution and a multiple comparison problem. In order to examine its performance, extensive experiments are done with synthetic data generated from multivariate normal distributions and a set of real image data.
This is a preview of subscription content, log in via an institution to check access.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
References
Benjamin, Y., Hochberg, Y.: Controlling the False Discovery Rate: a practical and powerful approach to multiple testing. J. R. Statist. Soc. B 57(1), 289–300 (1995)
Choi, K., Jun, C.: A systematic approach to the Kansei factors of tactile sense regarding the surface roughness. Applied Economics (in press, 2006)
Duda, R.D., Hart, P.E., Stork, D.G.: Pattern Classification. John Wiley & Sons, Inc., New York (2001)
Gallegos, M.T.: Maximum likelihood clustering with outliers. In: Jajuga, et al. (eds.) Classification, Clustering, and Data Analysis, Springer, Heidelberg (2002)
Gordon, A.: Classification, 2nd edn. Chapman and Hall-CRC, London (1999)
Hastie, T., Tibshirani, R., Friedman, J.: The elements of statistical learning. In: Data Mining, Inference, and Prediction, Springer, Heidelberg (2001)
Hotelling, H.: Multivariate Quality Control. In: Eisenhart, C., Hastay, M.W., Wallis, W.A. (eds.) Techniques of Statistical Analysis, McGraw-Hill, New York (1947)
Ihaka, R., Gentleman, R.: A language for data analysis and graphics. Journal of Computational and Graphical Statistics 5(3), 299–314 (1996)
Jajuga, K., Sokolowski, A., Bock, H.-H. (eds.): Classification, Clustering, and Data Analysis. Springer, Heidelberg (2002)
Kim, D.H., Chung, C.W., Barnard, K.: Relevance Feedback using Adaptive Clustering for Image Similarity Retrieval. The Journal of Systems and Software 78, 9–23 (2005)
Mardia, K.V., Kent, J.T., Bibby, J.M.: Multivariate Analysis. Academic Press, London (1979)
Miligan, G.W., Cooper, M.C.: An examination of procedure for determining the number of clusters in a data set. Psychometrika 50, 159–179 (1985)
Mojena, R.: Hierarchical grouping methods and stopping rules: An evaluation. The Computer journal 20(4) (1975)
Rencher, A.C.: Methods of Multivariate Analysis. John Wiley and Sons, Chichester (2002)
Rousseeuw, P.J., Van Driessen, K.: A first algorithm for the minimum covariance determinant estimator. Technometrics 41, 212–223 (1999)
Tibsirani, R., Walther, G., Hasite, T.: Estimating the number of clusters in a data set via the gap statistic. J.R. Statist. Soc. B 63, 411–423 (2001)
Ward, J.H.: Hierarchical Grouping to optimize an objective function. J. of Amer. Stat. Assoc. 58, 236–244 (1963)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2006 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Choi, K., Kim, DH., Choi, T. (2006). Estimating the Number of Clusters Using Multivariate Location Test Statistics. In: Wang, L., Jiao, L., Shi, G., Li, X., Liu, J. (eds) Fuzzy Systems and Knowledge Discovery. FSKD 2006. Lecture Notes in Computer Science(), vol 4223. Springer, Berlin, Heidelberg. https://doi.org/10.1007/11881599_43
Download citation
DOI: https://doi.org/10.1007/11881599_43
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-45916-3
Online ISBN: 978-3-540-45917-0
eBook Packages: Computer ScienceComputer Science (R0)