Abstract
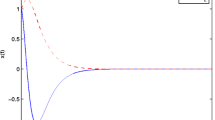
For the conservative and difficulty of checking the stability of discrete T-S fuzzy control system with the common Lyapunov function approach and the fuzzy Lyapunov function approach, a fuzzy controller is designed to acquire globally asymptotical stability for discrete fuzzy system with the method of parallel distributed compensation (PDC) after the definition of a piecewise fuzzy Lyapunov function. Then a new sufficient condition to check the stability of closed-loop discrete T-S fuzzy system is proposed and proved. This condition is less conservative and difficult than above approaches. At last, a simulation example shows that the approach is effective.
The work is supported by the Ministry of Communication of P.R. China (Grant #200332922505) and Doctoral Bases Foundation of the Educational Committee of P.R. China (Grant #20030151005).
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
Tanaka, K., Sugeno, M.: Stability Analysis and Design of Fuzzy Control System. Fuzzy Sets and Systems 45, 135–156 (1992)
Tanaka, K., Hori, T., Wang, H.O.: A Multiple Lyapunov Function Approach to Stabilization of Fuzzy Control Systems. IEEE Trans. Fuzzy Systems 11, 582–589 (2003)
Xiu, Z.H., Ren, G.: Stability Analysis and Systematic Design of Takagi-Sugeno Fuzzy Control Systems. Fuzzy Sets and Systems 151, 119–138 (2005)
Henon, M.: A Two Dimensional Map with A Strange Attractor. Math. Phys. 50, 69–73 (1976)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2006 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Yu, J., Zhang, S., Ren, G. (2006). Stability Analysis and Controller Design of Discrete T-S Fuzzy System. In: Wang, L., Jiao, L., Shi, G., Li, X., Liu, J. (eds) Fuzzy Systems and Knowledge Discovery. FSKD 2006. Lecture Notes in Computer Science(), vol 4223. Springer, Berlin, Heidelberg. https://doi.org/10.1007/11881599_6
Download citation
DOI: https://doi.org/10.1007/11881599_6
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-45916-3
Online ISBN: 978-3-540-45917-0
eBook Packages: Computer ScienceComputer Science (R0)