Abstract
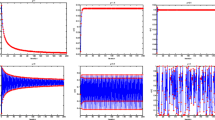
Chaotic neural networks have been proved to be powerful tools to solve the optimization problems. In order to escape the local minima, a new chaotic neural network model called Gauss Wavelet chaotic neural network was presented, and the chaotic mechanism is introduced by the attenuation of the self-feedback connection weight. The activation function of the new model is non-monotonous, which is composed of sigmoid function and Gauss Wavelet function. First, the figures of the reversed bifurcation and the maximal Lyapunov exponents of single neural unit were given. Second, the new model was applied to solve function optimizations. Finally, 10-city traveling salesman problem was given and the effects of the non-monotonous degree in the model on solving 10-city traveling salesman problem were discussed. The new model can solve the optimization problems more effectively because Gauss wavelet is a kind of basic function. Seen from the simulation results, the new model is powerful than the common chaotic neural network.
This is a preview of subscription content, log in via an institution to check access.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
References
Hopfield, J.J., Tank, D.W.: Neural Computation of Decision in Optimization Problems. Biol. Cybern. 52, 141–152 (1985)
Hopfield, J.: Neural Networks and Physical Systems with Emergent Collective Computational Abilities. Proc. Natl. Acad. Sci. 79, 2554–2558 (1982)
Xu, Y.-q., Sun, M., Duan, G.-r.: Wavelet Chaotic Neural Networks and Their Application to Optimization Problems. LNCS, vol. 3791, pp. 379–384. Springer, Heidelberg (2006)
Xu, Y.-q., Sun, M.: Gauss-Morlet-Sigmoid Chaotic Neural Networks. In: Huang, D.-S., Li, K., Irwin, G.W. (eds.) ICIC 2006. LNCS, vol. 4113, pp. 115–125. Springer, Heidelberg (2006)
Xu, Y.-q., Sun, M., Shen, J.-h.: Gauss Chaotic Neural Networks. In: Yang, Q., Webb, G. (eds.) PRICAI 2006. LNCS (LNAI), vol. 4099, pp. 319–328. Springer, Heidelberg (2006)
Potapove, A., Kali, M.: Robust chaos in neural networks. Physics Letters A 277(6), 310–322 (2000)
Shuai, J.W., Chen, Z.X., Liu, R.T., et al.: Self-evolution Neural Model. Physics Letters A 221(5), 311–316 (1996)
Chen, L., Aihara, K.: Chaotic Simulated Annealing by a Neural Network Model with Transient Chaos. Neural Networks 8(6), 915–930 (1995)
Ling, W.: Intelligence optimization algorithm and its application. Press of TUP (2001)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2006 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Xu, Yq., Sun, M., Shen, Jh. (2006). Gauss Wavelet Chaotic Neural Networks. In: King, I., Wang, J., Chan, LW., Wang, D. (eds) Neural Information Processing. ICONIP 2006. Lecture Notes in Computer Science, vol 4232. Springer, Berlin, Heidelberg. https://doi.org/10.1007/11893028_52
Download citation
DOI: https://doi.org/10.1007/11893028_52
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-46479-2
Online ISBN: 978-3-540-46480-8
eBook Packages: Computer ScienceComputer Science (R0)