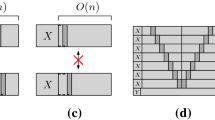
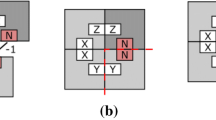
Abstract
In this paper we construct fixed finite tile systems that assemble into particular classes of shapes. Moreover, given an arbitrary n, we show how to calculate the tile concentrations in order to ensure that the expected size of the produced shape is n. For rectangles and squares our constructions are optimal (with respect to the size of the systems). We also introduce the notion of parallel time, which is a good approximation of the classical asynchronous time. We prove that our tile systems produce the rectangles and squares in linear parallel time (with respect to the diameter). Those results are optimal. Finally, we introduce the class of diamonds. For these shapes we construct a non trivial tile system having also a linear parallel time complexity.
This work was supported by programs Ecos-Conicyt, Conicyt “Anillo en Redes”, and Fondap on Applied Mathematics.
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
Adleman, L., Cheng, Q., Goel, A., Huang, M.: Running time and program size for self-assembled squares. In: Proceedings of the 33rd Annual ACM Symposium on Theory of Computing (STOC 2001), pp. 740–748 (2001)
Aggarwal, G., Goldwasser, M.H., Kao, M.-Y., Schweller, R.T.: Complexities for generalized models of self-assembly. In: Proceedings of the 15th Annual ACM-SIAM Symposium on Discrete Algorithms (SODA 2004), pp. 880–889 (2004)
Mazoyer, J., Reimen, N.: A linear speed-up theorem for cellular automata. Theoretical Computer Science 101, 59–98 (1992)
Rothemund, P.: Theory and experiments in algorithmic self-assembly. Ph. D. Thesis, University of Southern California (2001)
Rothemund, P., Winfree, E.: The program size complextity of self-assembled squares. In: Proceedings of the 32nd Annual ACM Symposium on Theory of Computing (STOC 2000), pp. 459–468 (2000)
Wang, H.: Proving theorems by pattern recognition. H. Bell System Technical Journal 40, 1–41 (1961)
Winfree, E.: Algorithmic self-assembly of DNA. Ph.D. thesis, California Institute of Technology, Pasadena (1998)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2006 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Becker, F., Rapaport, I., Rémila, É. (2006). Self-assemblying Classes of Shapes with a Minimum Number of Tiles, and in Optimal Time. In: Arun-Kumar, S., Garg, N. (eds) FSTTCS 2006: Foundations of Software Technology and Theoretical Computer Science. FSTTCS 2006. Lecture Notes in Computer Science, vol 4337. Springer, Berlin, Heidelberg. https://doi.org/10.1007/11944836_7
Download citation
DOI: https://doi.org/10.1007/11944836_7
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-49994-7
Online ISBN: 978-3-540-49995-4
eBook Packages: Computer ScienceComputer Science (R0)