Skip to main content
Springer Nature Link
Log in

Approximation Algorithms for Scheduling Problems with Exact Delays

  • Conference paper
Approximation and Online Algorithms (WAOA 2006)

Part of the book series: Lecture Notes in Computer Science ((LNTCS,volume 4368))

Included in the following conference series:

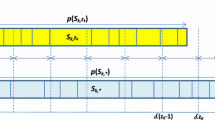
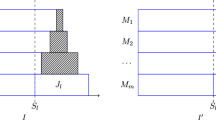
Abstract

We give first constant-factor approximations for various cases of the coupled-task single machine and two-machine flow shop scheduling problems with exact delays and makespan as the objective function. In particular, we design 3.5- and 3-approximation algorithms for the general cases of the single-machine and the two-machine problems, respectively. We also prove that the existence of a (2−ε)-approximation algorithm for the single-machine problem as well as the existence of a (1.5−ε)-approximation algorithm for the two-machine problem implies P=NP. The inapproximability results are valid for the cases when the operations of each job have equal processing times and for these cases the approximation ratios achieved by our algorithms are very close to best possible: we prove that the single machine problem is approximable within a factor of 2.5 and the two-machine problem is approximable within a factor of 2.

Research supported by the Russian Foundation for Basic Research, projects 05-01-00960, 06-01-00255.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution

Institutional subscriptions

Preview

Unable to display preview. Download preview PDF.

Unable to display preview. Download preview PDF.

Similar content being viewed by others

References

  1. Ageev, A.A., Baburin, A.E.: Approximation Algorithms for the Single and Two-Machine Scheduling Problems with Exact Delays. To appear in Operations Research Letters

    Google Scholar 

  2. Farina, A., Neri, P.: Multitarget interleaved tracking for phased array radar. IEEE Proc. Part F: Comm. Radar Signal Process 127(4), 312–318 (1980)

    Article  Google Scholar 

  3. Garey, M.R., Johnson, D.S.: Computers and intractability: A guide to the theory of NP-completeness. Freeman, San Francisco (1979)

    MATH  Google Scholar 

  4. Elshafei, M., Sherali, H.D., Smith, J.C.: Radar pulse interleaving for multi-target tracking. Naval Res. Logist. 51, 79–94 (2004)

    Article  MathSciNet  Google Scholar 

  5. Izquierdo-Fuente, A., Casar-Corredera, J.R.: Optimal radar pulse scheduling using neural networks. IEEE International Conference on Neural Networks 7, 4588–4591 (1994)

    MATH  Google Scholar 

  6. Graham, R.L., Lawler, E.L., Lenstra, J.K., Rinnooy Kan, A.H.G.: Optimization and approximation in deterministic sequencing and scheduling: a survey. Annals of Discrete Mathematics 5, 287–326 (1979)

    Article  MATH  MathSciNet  Google Scholar 

  7. Orman, A.J., Potts, C.N.: On the complexity of coupled-task scheduling. Discrete Appl. Math. 72, 141–154 (1997)

    Article  MATH  MathSciNet  Google Scholar 

  8. Sherali, H.D., Smith, J.C.: Interleaving two-phased jobs on a single machine. Discrete Optimization 2, 348–361 (2005)

    Article  MATH  MathSciNet  Google Scholar 

  9. Yu, W.: The two-machine shop problem with delays and the one-machine total tardiness problem, Ph.D. thesis, Technische Universiteit Eindhoven (1996)

    Google Scholar 

  10. Yu, W., Hoogeveen, H., Lenstra, J.K.: Minimizing makespan in a two-machine flow shop with delays and unit-time operations is NP-hard. J. Sched. 7(5), 333–348 (2004)

    Article  MATH  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Sobolev Institute of Mathematics, pr. Koptyuga 4, Novosibirsk, Russia

    Alexander A. Ageev & Alexander V. Kononov

Authors
  1. Alexander A. Ageev
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Alexander V. Kononov
    View author publications

    You can also search for this author in PubMed Google Scholar

Editor information

Editors and Affiliations

  1. Department of Computer Science, University of Leicester, University Road, LE1 7RH, Leicester, UK

    Thomas Erlebach

  2. Research Academic Computer Technology Institute &, Department of Computer Engineering and Informatics, University of Patras, 26500, Rio, Greece

    Christos Kaklamanis

Rights and permissions

Reprints and permissions

Copyright information

© 2007 Springer-Verlag Berlin Heidelberg

About this paper

Cite this paper

Ageev, A.A., Kononov, A.V. (2007). Approximation Algorithms for Scheduling Problems with Exact Delays. In: Erlebach, T., Kaklamanis, C. (eds) Approximation and Online Algorithms. WAOA 2006. Lecture Notes in Computer Science, vol 4368. Springer, Berlin, Heidelberg. https://doi.org/10.1007/11970125_1

Download citation

  • DOI: https://doi.org/10.1007/11970125_1

  • Publisher Name: Springer, Berlin, Heidelberg

  • Print ISBN: 978-3-540-69513-4

  • Online ISBN: 978-3-540-69514-1

  • eBook Packages: Computer ScienceComputer Science (R0)

Publish with us

Policies and ethics