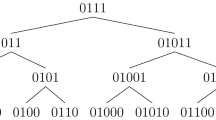
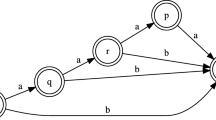
Abstract
We describe a deterministic parallel algorithm to compute algebraic expressions in log n time using n/log(n) processors on a parallel random access machine without write conflicts (P-RAM) with no free preprocessing. The input to our algorithm is a string, given by an array, of the expression. Such a form for the input enables a consecutive numbering of the operands in the expression in log(n) time with n/log(n) processors. This corresponds to a consecutive numbering of leaves in the tree of the expression which further enables a suitable partitioning of the leaves into small segments. We improve the result of Miller and Reif (1985), who described an optimal parallel randomized algorithm. Our algorithm can be used to construct optimal parallel algorithms for the recognition of two nontrivial subclasses of context-free languages: bracket and input-driven languages. These languages are the most complicated context-free languages known to be recognizable in deterministic logarithmic space. This strengthens the result of Matheyses and Fiduccia (1982) who constructed an almost optimal parallel algorithm for Dyck languages, since Dyck languages are a proper subclass of input-driven languages.
Using our algorithm we show also that preorder and postorder numberings of the nodes of a tree (whose leaves are already consecutively numbered) can be computed by optimal parallel algorithms.
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
I. Bar-On, and U. Vishkin, (1985), Optimal parallel generation of a computation tree form. ACM trans.on Progr.Lang.and Systems 7,2,348–357
B.Braunmuhl, and R.Verbeek (1983), Recognizing input-driven languages in l og n space, Fund.of Comp.Theory,Lect.Notes in Computer Science
R.P. Brent (1974), The parallel evaluation of general arithmetic expressions. JACM 21,2,201–208
R.Giancarlo, and W.Rytter (1985), Parallel recognition of input driven and parsing of bracket languages, manuscript, University of Salerno, Dept.of Informatics
G. Kindervater and J. Lenstra (1985), An introduction to parallelism in combinatorial optimization. Report OS-R8501, Centre for Mathematics and Computer Science, Amsterdam
Ming-Deh A. Huang (1985), Solving some graph problems with optimal or near optimal speed up on mesh-of-trees networks. 26th IEEE Symp. on Found.of Comp.Science, 232–240
R.Matheyses, and C.M.Fiduccia (1982), Parsing Dyck languages on parallel machines. 20th Allerton Conference on Comm.Control and Computing
G.L.Miller, and J.Reif (1985), Parallel tree contraction and its application. 26th IEEE Symp. on Found.of Comp.Science, 478–489
W.Rytter (1984), An application of Mehlhorn's algorithm for bracket languages to log n space recognition of input driven languages, Berichte Theoretische Informatik, Fachb.Math.Informatik, Universitat Paderborn (to appear in Inf.Process.Letters, 1986)
W.Rytter (1985a), Parallel time 0(log n) recognition of unambiguous cfl's. Fund.of Computation Theory, Lect.Notes in Comp.Science
W.Rytter (1985b), The complexity of two way pushdown automata and recursive programs. Combinatorial algorithms on words (ed.A.Apostolica, Z.Galil), NATO ASI Series F:12, Springer Verlag
W.Rytter (1985c), Remarks on pebble games on graphs. In Combinatorial Analysis and Its Applications (ed.M.Syslo), to appear in Lect.Notes in Mathematics
W.Rytter (1985d), On the recognition of context free languages, Lect. Notes in Comp.Science 208
R.E.Tarjan, and U.Vishkin (1984), Finding biconnected components and computing tree functions in logarithmic parallel time. 25th Symp.on Found.of Computer Science, IEEE, 12–22.
Author information
Authors and Affiliations
Editor information
Rights and permissions
Copyright information
© 1986 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Gibbons, A., Rytter, W. (1986). An optimal parallel algorithm for dynamic expression evaluation and its applications. In: Nori, K.V. (eds) Foundations of Software Technology and Theoretical Computer Science. FSTTCS 1986. Lecture Notes in Computer Science, vol 241. Springer, Berlin, Heidelberg. https://doi.org/10.1007/3-540-17179-7_28
Download citation
DOI: https://doi.org/10.1007/3-540-17179-7_28
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-17179-9
Online ISBN: 978-3-540-47239-1
eBook Packages: Springer Book Archive