Skip to main content
SpringerLink
Log in

Some Open Problem Sets for Generalized Blockmodeling

  • Conference paper
Data Science and Classification

Abstract

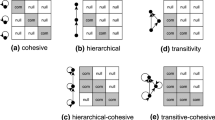
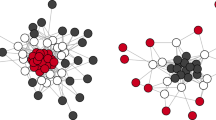
This paper provides an introduction to the blockmodeling problem of how to cluster networks, based solely on the structural information contained in the relational ties, and a brief overview of generalized blockmodeling as an approach for solving this problem. Following a formal statement of the core of generalized blockmodeling, a listing of the advantages of adopting this approach to partitioning networks is provided. These advantages, together with some of the disadvantages of this approach, in its current state, form the basis for proposing some open problem sets for generalized blockmodeling. Providing solutions to these problem sets will transform generalized blockmodeling into an even more powerful approach for clustering networks of relations.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution
Chapter
USD 29.95
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever
eBook
USD 129.00
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever
Softcover Book
USD 169.99
Price excludes VAT (USA)
  • Compact, lightweight edition
  • Dispatched in 3 to 5 business days
  • Free shipping worldwide - see info

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Preview

Unable to display preview. Download preview PDF.

Unable to display preview. Download preview PDF.

References

  • BAKER, W. E. (1986): Three-dimensional blockmodeling. Journal of Mathematical Sociology,12, 191–223.

    Article  MATH  Google Scholar 

  • BATAGELJ, V., DOREIAN, P. and FERLIGOJ, A. (2006): Three dimensional blockmodeling. International Sunbelt XXVI Social Network Conference, Vancouver, Canada, April 25–30.

    Google Scholar 

  • BATAGELJ, V., DOREIAN, P. and FERLIGOJ, A. (1992a): An optimization approach to regular equivalence. Social Networks, 14, 121–135.

    Article  Google Scholar 

  • BATAGELJ, V., FERLIGOJ, A. and DOREIAN, P. (1992b): Direct and indirect methods for structural equivalence. Social Networks, 14, 63–90.

    Article  Google Scholar 

  • BATAGELJ, V. and MRVAR, A. (1998): Pajek — Program for large network analysis. Connections, 21(2), 47–57. See also http://vlado.fmf.unilj.si/pub/networks/pajek for documentation and the most recent version of this program.

    Google Scholar 

  • BORGATTI, S. P. and EVERETT, M. (1989) The class of regular equivalences: Algebraic structure and computation. Social Networks, 11, 65–88.

    Article  MathSciNet  Google Scholar 

  • BREIGER, R. L., BOORMAN, S. A. and ARABIE, P. (1975): An algorithm for clustering relational data with applications to social network analysis and comparison to multidimensional scaling. Journal of Mathematical Psychology, 12, 328–383.

    Article  Google Scholar 

  • BURT, R. S. (1976): Positions in networks. Social Forces, 55, 93–122.

    Article  MathSciNet  Google Scholar 

  • DAVIS J. A. and LEINHARDT, S. (1972): The structure of positive interpersonal relations in small groups. In: J. Berger, M. Zelditch Jr and B. Anderson (Eds) Sociological Theories in Progress, Volume 2. Houghton Mifflin, Boston, 218–251.

    Google Scholar 

  • DOREIAN, P.(1993): A measure of standing for citation networks within a wider environment. Information Processing and Management, 30/1, 21–31.

    Google Scholar 

  • DOREIAN, P., BATAGELJ, V. and FERLIGOJ, A. (2005): Generalized Blockmodeling. University of Cambridge, New York.

    Google Scholar 

  • DOREIAN, P., BATAGELJ, V. and FERLIGOJ, A. (2000): Symmetric-Acyclic Decompositions of Networks. Journal of Classification, 17/1, 3–28.

    Article  MathSciNet  MATH  Google Scholar 

  • DOREIAN, P., BATAGELJ, V. and FERLIGOJ, A. (1994): Partitioning networks based on generalized concepts of equivalence. Journal of Mathematical Sociology, 19, 1–27.

    Article  MATH  Google Scholar 

  • DOREIAN, P. and MRVAR A. (1996): A partitioning approach to structural balance. Social Networks, 18, 149–168.

    Article  Google Scholar 

  • DOREIAN, P. and STOKMAN, F. N. (Eds.) (1997): Social Network Evolution Gordon and Breach, New York.

    Google Scholar 

  • DOREIAN, P. and WOODARD, K. L. (1994): Defining and locating cores and boundaries of social networks. Social Networks, 16, 267–293.

    Article  Google Scholar 

  • HEIDER, F. (1946): Attitudes and cognitive organization Journal of Psychology, 21, 107–112.

    Google Scholar 

  • HUMMON, N. P. and CARLEY, K (1993) Social networks as normal science Social Networks, 15, 71–106.

    Article  Google Scholar 

  • LAUMANN E. O., MARSDEN, P., V. and PRENSKY, D. (1983): The boundary specification problem in network analysis. In: R. S. Burt and M. J. Minor (Eds) Applied Network Analysis: A Methodological Introduction Sage, Beverly Hills, 18–34.

    Google Scholar 

  • LORRAIN, F. and WHITE, H. C. (1971): Structural equivalence of individuals in social networks. Journal of Mathematical Sociology, 1, 49–80.

    Article  Google Scholar 

  • SAILER, L. D. (1978): Structural equivalence: Meaning and definition, computation and application. Social Networks, 1, 73–90.

    Article  Google Scholar 

  • WHITE, D. R. and REITZ, K. P. (1983): Graph and semigroup homomorphisms on networks of relations. Social Networks, 5, 193–234

    Article  MathSciNet  Google Scholar 

  • WINSHIP, C. and MANDEL, M (1983): Roles and positions: A critique and extension of the blockmodeling approach. In S. Leinhardt (Ed.) Sociological Methodology 1983–4 Jossey-Bass, San Francisco, 314–344.

    Google Scholar 

  • ŽIBERNA, A. (2005): Generalized blockmodeling of valued networks. University of Ljubljana, Slovenia.

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Sociology, University of Pittsburgh, 2603 WWPH, Pittsburgh, PA, 15260, USA

    Patrick Doreian

Authors
  1. Patrick Doreian
    View author publications

    You can also search for this author in PubMed Google Scholar

Editor information

Editors and Affiliations

  1. Department of Mathematics, FMF, University of Ljubljana, Jadranska 19, 1000, Ljubljana, Slovenia

    Vladimir Batagelj

  2. Institute of Statistics, RWTH Aachen University, 52056, Aachen, Germany

    Hans-Hermann Bock

  3. Faculty of Social Sciences, University of Ljubljana, Kardeljeva pl. 5, 1000, Ljubljana, Slovenia

    Anuška Ferligoj  & Aleš Žiberna  & 

Rights and permissions

Reprints and permissions

Copyright information

© 2006 Springer-Verlag Berlin · Heidelberg

About this paper

Cite this paper

Doreian, P. (2006). Some Open Problem Sets for Generalized Blockmodeling. In: Batagelj, V., Bock, HH., Ferligoj, A., Žiberna, A. (eds) Data Science and Classification. Studies in Classification, Data Analysis, and Knowledge Organization. Springer, Berlin, Heidelberg . https://doi.org/10.1007/3-540-34416-0_14

Download citation

Publish with us

Policies and ethics

Search

Navigation