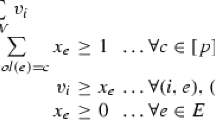Skip to main content
SpringerLink
Log in

On the Hardness of Constructing Minimal 2-Connected Spanning Subgraphs in Complete Graphs with Sharpened Triangle Inequality

Extended Abstract

  • Conference paper
  • First Online:
Book cover FST TCS 2002: Foundations of Software Technology and Theoretical Computer Science (FSTTCS 2002)

Part of the book series: Lecture Notes in Computer Science ((LNCS,volume 2556))

Abstract

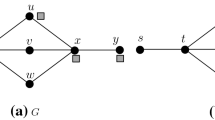
In this paper we investigate the problem of finding a 2- connected spanning subgraph of minimal cost in a complete and weighted graph G. This problem is known to be APX-hard, both for the edge- and for the vertex-connectivity case. Here we prove that the APX-hardness still holds even if one restricts the edge costs to an interval [1,1 + ε], for an arbitrary small ε > 0. This result implies the first explicit lower bound on the approximability of the general problems.

On the other hand, if the input graph satisfies the sharpened β-triangle inequality, then a (2/3 + 1/3 . β/1-β)-approximation algorithm is designed. This ratio tends to 1 with β tending to 1/2, and it improves the previous known bound of 3/2, holding for graphs satisfying the triangle inequality, as soon as β < 5/7.

Furthermore, a generalized problem of increasing to 2 the edge-connectivity of any spanning subgraph of G by means of a set of edges of minimum cost is considered. This problem is known to admit a 2-approximation algorithm. Here we show that whenever the input graph satisfies the sharpened β-triangle inequality with β < 2/3, then this ratio can be improved to β/1-β.

This work was partially supported by DFG-grant Hr 14/5-1, the CNR-Agenzia 2000 Program, under Grants No. CNRC00CAB8 and CNRG003EF8, and the Research Project REAL-WINE, partially funded by the Italian Ministry of Education, University and Research.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution
Chapter
USD 29.95
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever
eBook
USD 39.99
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever
Softcover Book
USD 54.99
Price excludes VAT (USA)
  • Compact, lightweight edition
  • Dispatched in 3 to 5 business days
  • Free shipping worldwide - see info

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Preview

Unable to display preview. Download preview PDF.

Unable to display preview. Download preview PDF.

References

  1. T. Andreae: On the traveling salesman problem restricted to inputs satisfying a relaxed triangle inequality. Networks 38(2) (2001), pp. 59–67.

    Article  MATH  MathSciNet  Google Scholar 

  2. T. Andreae, H.-J. Bandelt: Performance guarantees for approximation algorithms depending on parametrized triangle inequalities. SIAM Journal on Discrete Mathematics 8 (1995), pp. 1–16.

    Article  MATH  MathSciNet  Google Scholar 

  3. G. Ausiello, P. Crescenzi, G. Gambosi, V. Kann, A. Marchetti-Spaccamela, M. Protasi: Complexity and Approximation: Combinatorial Optimization Problems and their Approximability Properties. Springer 1999.

    Google Scholar 

  4. M. A. Bender, C. Chekuri: Performance guarantees for the TSP with a parameterized triangle inequality. Information Processing Letters 73 (2000), pp. 17–21.

    Article  MathSciNet  Google Scholar 

  5. H.-J. Böckenhauer, J. Hromkovič, R. Klasing, S. Seibert, W. Unger: Approximation algorithms for the TSP with sharpened triangle inequality. Information Processing Letters 75, 2000, pp. 133–138.

    Article  MathSciNet  Google Scholar 

  6. H.-J. Böckenhauer, J. Hromkovič, R. Klasing, S. Seibert, W. Unger: Towards the Notion of Stability of Approximation for Hard Optimization Tasks and the Traveling Salesman Problem (Extended Abstract). Proc. CIAC 2000, LNCS 1767, Springer 2000, pp. 72–86. Full version in Theoretical Computer Science 285(1) (2002), pp. 3–24.

    Google Scholar 

  7. H.-J. Böckenhauer, J. Hromkovič, R. Klasing, S. Seibert, W. Unger: An Improved Lower Bound on the Approximability of Metric TSP and Approximation Algorithms for the TSP with Sharpened Triangle Inequality (Extended Abstract). Proc. STACS 2000, LNCS 1770, Springer 2000, pp. 382–394.

    Google Scholar 

  8. H.-J. Böckenhauer, S. Seibert: Improved lower bounds on the approximability of the traveling salesman problem. RAIRO-Theoretical Informatics and Applications 34, 2000, pp. 213–255.

    Article  MATH  Google Scholar 

  9. A. Czumaj, A. Lingas: On approximability of the minimum-cost k-connected spanning subgraph problem. Proc. SODA’99, 1999, pp. 281–290.

    Google Scholar 

  10. L. S. Chandran, L. S. Ram: Approximations for ATSP with Parametrized Triangle Inequality. Proc. STACS 2002, LNCS 2285, Springer 2002, pp. 227–237.

    Google Scholar 

  11. R. G. Downey, M. R. Fellows: Fixed-parameter tractability and completeness. Congressus Numerantium 87 (1992), pp. 161–187.

    MathSciNet  Google Scholar 

  12. R. G. Downey, M. R. Fellows: Parameterized Complexity. Springer 1999.

    Google Scholar 

  13. K. P. Eswaran, R. E. Tarjan: Augmentation Problems. SIAM Journal on Computing 5(4), 1976, pp. 653–665.

    Article  MATH  MathSciNet  Google Scholar 

  14. C. G. Fernandes: A better approximation ratio for the minimum size k-edgeconnected spanning subgraph problem. J. Algorithms, 28(1) (1998), pp. 105–124.

    Article  MATH  MathSciNet  Google Scholar 

  15. G. N. Frederickson, J. Jájá: On the relationship between the biconnectivity augmentation and traveling salesman problems. Theoretical Computer Science, 19 (1982), pp. 189–201.

    Article  MATH  MathSciNet  Google Scholar 

  16. A. Galluccio, G. Proietti: Polynomial time algorithms for edge-connectivity augmentation of Hamiltonian paths. Proc. ISAAC’01, LNCS 2223, Springer 2001, pp. 345–354.

    Google Scholar 

  17. M. R. Garey, D. S. Johnson: Computers and Intractability: A guide to the theory of NP-completeness. W. H. Freeman and Company, San Francisco, 1979.

    MATH  Google Scholar 

  18. M. Grötschel, L. Lovász, A. Schrijver: Geometric Algorithms and Combinatorial Optimization. Springer 1988.

    Google Scholar 

  19. M. Grötschel, C.L. Monma, M. Stoer: Design of survivable networks. Handbooks in OR and MS, Vol. 7, Elsevier (1995), pp. 617–672.

    Article  Google Scholar 

  20. J. Hromkovič: Algorithmics for Hard Problems-Introduction to Combinatorial Optimization, Randomization, Approximation, and Heuristics. Springer 2001.

    Google Scholar 

  21. P. Krysta, V. S. A. Kumar: Approximation algorithms for minimum size 2-connectivity problems. Proc. STACS 2001, LNCS 2010, Springer 2001, pp. 431–442.

    Google Scholar 

  22. S. Khuller, R. Thurimella: Approximation algorithms for graph augmentation. Journal of Algorithms 14 (1993), pp. 214–225.

    Article  MATH  MathSciNet  Google Scholar 

  23. S. Khuller, U. Vishkin: Biconnectivity approximations and graph carvings. Journal of the ACM 41 (1994), pp. 214–235.

    Article  MATH  MathSciNet  Google Scholar 

  24. H. Nagamochi, T. Ibaraki: An approximation for finding a smallest 2-edgeconnected subgraph containing a specified spanning tree. Proc. COCOON’99, LNCS 1627, Springer 1999, pp. 31–40.

    Google Scholar 

  25. M. Penn, H. Shasha-Krupnik: Improved approximation algorithms for weighted 2-and 3-vertex connectivity augmentation. Journal of Algorithms 22 (1997), pp. 187–196.

    Article  MATH  MathSciNet  Google Scholar 

  26. S. Vempala, A. Vetta: Factor 4/3 approximations for minimum 2-connected subgraphs. Proc. APPROX 2000, LNCS 1913, Springer 2000, pp. 262–273.

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Lehrstuhl für Informatik I, RWTH Aachen, 52074, Aachen, Germany

    Hans-Joachim Böckenhauer, Dirk Bongartz, Juraj Hromkovič, Sebastian Seibert & Walter Unger

  2. Department of Computer Science, King’s College London Strand, WC2R 2LS, London, UK

    Ralf Klasing

  3. Dipartimento di Informatica, Università di L’Aquila, 67010 L’Aquila, Italy and Istituto di Analisi dei Sistemi ed Informatica “Antonio Ruberti”, Roma, CNR, Italy

    Guido Proietti

Authors
  1. Hans-Joachim Böckenhauer
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Dirk Bongartz
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Juraj Hromkovič
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Ralf Klasing
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Guido Proietti
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Sebastian Seibert
    View author publications

    You can also search for this author in PubMed Google Scholar

  7. Walter Unger
    View author publications

    You can also search for this author in PubMed Google Scholar

Editor information

Editors and Affiliations

  1. Department of Computer Science and Engineering, Indian Institute of Technology, 208016, Kanpur, India

    Manindra Agrawal  & Anil Seth  & 

Rights and permissions

Reprints and permissions

Copyright information

© 2002 Springer-Verlag Berlin Heidelberg

About this paper

Cite this paper

Böckenhauer, HJ. et al. (2002). On the Hardness of Constructing Minimal 2-Connected Spanning Subgraphs in Complete Graphs with Sharpened Triangle Inequality. In: Agrawal, M., Seth, A. (eds) FST TCS 2002: Foundations of Software Technology and Theoretical Computer Science. FSTTCS 2002. Lecture Notes in Computer Science, vol 2556. Springer, Berlin, Heidelberg. https://doi.org/10.1007/3-540-36206-1_7

Download citation

  • DOI: https://doi.org/10.1007/3-540-36206-1_7

  • Published:

  • Publisher Name: Springer, Berlin, Heidelberg

  • Print ISBN: 978-3-540-00225-3

  • Online ISBN: 978-3-540-36206-7

  • eBook Packages: Springer Book Archive

Publish with us

Policies and ethics

Search

Navigation