Abstract
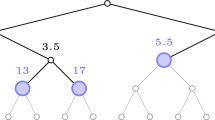
We introduce a novel technique for computation of consecutive preimages of hash chains. Whereas traditional techniques have a memory-times-computation complexity of O(n) per output generated, the complexity of our technique is only O(log2 n), where n is the length of the chain.
Our solution is based on the same principal amortization principle as [2], and has the same asymptotic behavior as this solution. However, our solution decreases the real complexity by approximately a factor of two. Thus, the computational costs of our solution are approximately 1/2log2 n hash function applications, using only a little more than log2 n storage cells.
A result of independent interest is the lower bounds we provide for the optimal (but to us unknown) solution to the problem we study. The bounds show that our proposed solution is very close to optimal. In particular, we show that there exists no improvement on our scheme that reduces the complexity by more than an approximate factor of two.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
G. Itkis and L. Reyzin, “Forward-Secure Signatures with Optimal Signing and Verifying,” Crypto’ 01, pp. 332–354.
M. Jakobsson, “Fractal Hash Sequence Representation and Traversal,” ISIT’ 02; full paper at http://www.markus-jakobsson.com.
M. Jakobsson “Method and Apparatus for Efficient Computation of One-Way Chains in Cryptographic Applications,” U.S. Patent Application 09/969,833
L. Lamport, “Constructing Digital Signatures from a One Way Function,” SRI International Technical Report CSL-98 (October 1979).
R. Merkle, “A digital signature based on a conventional encryption function,” Proceedings of Crypto’ 87.
S. Micali, “Efficient Certificate Revocation,” Proceedings of RSA’ 97, and U.S. Patent No. 5,666,416.
A. Perrig, R. Canetti, D. Song, and D. Tygar, “Efficient and Secure Source Authentication for Multicast,” Proceedings of Network and Distributed System Security Symposium NDSS 2001, February 2001.
A. Perrig, R. Canetti, D. Song, and D. Tygar, “Efficient Authentication and Signing of Multicast Streams over Lossy Channels,” Proc. of IEEE Security and Privacy Symposium S & P 2000, May 2000.
A. Perrig, R. Canetti, D. Song, and D. Tygar, “TESLA: Multicast Source Authentication Transform”, Proposed IRTF draft, http://paris.cs.berkeley.edu/~perrig/
K. S. J. Pister, J. M. Kahn and B. E. Boser, “Smart Dust: Wireless Networks of Millimeter-Scale Sensor Nodes. Highlight Article in 1999 Electronics Research Laboratory Research Summary.”, 1999. See http://robotics.eecs.berkeley.edu/~pister/SmartDust/
FIPS PUB 180-1, “Secure Hash Standard, SHA-1,” http://www.itl.nist.gov/fipspubs/fip180-l.htm
S. Stubblebine and P. Syverson, “Fair On-line Auctions Without Special Trusted Parties,” Financial Cryptography’ 01.
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2003 IFCA/Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Coppersmith, D., Jakobsson, M. (2003). Almost Optimal Hash Sequence Traversal. In: Blaze, M. (eds) Financial Cryptography. FC 2002. Lecture Notes in Computer Science, vol 2357. Springer, Berlin, Heidelberg. https://doi.org/10.1007/3-540-36504-4_8
Download citation
DOI: https://doi.org/10.1007/3-540-36504-4_8
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-00646-6
Online ISBN: 978-3-540-36504-4
eBook Packages: Springer Book Archive