Abstract
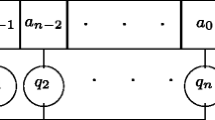
The problem of characterizing the randomness of finite sequences arises in cryptographic applications. The idea of randomness clearly reflects the difficulty of predicting the next digit of a sequence from all the previous ones. The approach taken in this paper is to measure the (linear) unpredictability of a sequence (finite or periodic) by the length of the shortest linear feedback shift register (LFSR) that is able to generate the given sequence. This length is often referred to in the literature as the linear complexity of the sequence. It is shown that the expected linear complexity of a sequence of n independent and uniformly distributed binary random variables is very close to n/2 and, that the variance of the linear complexity is virtually independent of the sequence length, i.e. is virtually a constant! For the practically interesting case of periodically repeating a finite truly random sequence of length 2m or 2m−1, it is shown that the linear complexity is close to the period length.
Chapter PDF
Similar content being viewed by others
References
Dai 85 Zong-duo Dai, “Proof of Rueppel’s Linear Complexity Conjecture”, submitted for publication in IEEE Trans. on Info. Th.
Fell 68 W. Feller, “An Introduction to Probability Theory and its Applications”, Vol. 1, John Wiley, 1968.
Golo 67 S.W. Golomb, “Shift Register Sequences”, Holden-Day, San Francisco, Calif., 1967.
Knut 81 D.E. Knuth, “The Art of Computer Programming, Vol. 2: Seminumberical Algorithms”, Addison-Wesley, 1981.
Kolm 65 A.N. Kolmogorov, “Three Approaches to the Quantitative Definition of Information”, Probl. Inform. Transmission, Vol. 1, 1965.
Lemp 76 A. Lempel, J. Ziv, “On the Complexity of Finite Sequences”, IEEE Trans. on Info. Theory, IT-22, Jan. 1976.
Mart 66 P. Martin-Loef, “The Definition of Random Sequences”, Information and Control, Vol. 9, 602–619, 1966.
Mass 69 J.L. Massey, “Shift-Register Synthesis and BCH Decoding”, IEEE Trans. on Info. Theory, Vol. IT-15, Jan. 1969.
Solo 64 R.J. Solomonov, “A Formal Theory of Inductive Inference”, Part I, Inform. Control 7, 1964.
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 1986 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Rueppel, R.A. (1986). Linear Complexity and Random Sequences. In: Pichler, F. (eds) Advances in Cryptology — EUROCRYPT’ 85. EUROCRYPT 1985. Lecture Notes in Computer Science, vol 219. Springer, Berlin, Heidelberg. https://doi.org/10.1007/3-540-39805-8_21
Download citation
DOI: https://doi.org/10.1007/3-540-39805-8_21
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-16468-5
Online ISBN: 978-3-540-39805-9
eBook Packages: Springer Book Archive