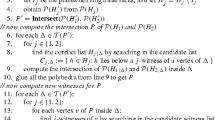Skip to main content
Springer Nature Link
Log in

Reporting Intersecting Pairs of Polytopes in Two and Three Dimensions

  • Conference paper
  • First Online:
Algorithms and Data Structures (WADS 2001)

Part of the book series: Lecture Notes in Computer Science ((LNCS,volume 2125))

Included in the following conference series:

  • 890 Accesses

Abstract

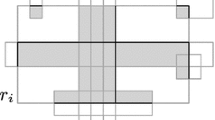
Let P={P 1,...,P m} be a set of m convex polytopes in ℝd, for d = 2,3, with a total of n vertices. We present output-sensitive algorithms for reporting all k pairs of indices (i, j) such that P i intersects P j. For the planar case we describe a simple algorithm with running time O(n 4/3logn + k), and an improved randomized algorithm with expected running time O((n log m + k)α(n)logn) (which is faster for small values of k). For d = 3, we present an O(n 8/5+ε + k)-time algorithm, for any ε>0. Our algorithms can be modified to count the number of intersecting pairs in O(n 4/3 logO(1) n) time for the planar case, and in O(n 8/5+ε) time and ℝ3.

P.A. was also supported by Army Research Office MURI grant DAAH04-96-1-0013, by a Sloan fellowship, by NSF grants EIA-9870724, EIA-997287, and CCR-9732787, and by a grant from the U.S.-Israeli Binational Science Foundation. M.S. was supported by NSF Grant CCR-97-32101, by a grant from the Israel Science Fund (for a Center of Excellence in Geometric Computing), by the Hermann Minkowski-MINERVA Center for Geometry at Tel Aviv University, and by a grant from the U.S.-Israeli Binational Science Foundation.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Chapter
USD 29.95
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Preview

Unable to display preview. Download preview PDF.

Unable to display preview. Download preview PDF.

Similar content being viewed by others

References

  1. P. Agarwal, Partitioning arrangements of lines: II. Applications, Discrete Comput. Geom., 5 (1990), 533–573.

    Article  MATH  MathSciNet  Google Scholar 

  2. P. K. Agarwal and J. Matousek, On range searching with semialgebraic sets, Discrete Comput. Geom., 11 (1994), 393–418.

    Article  MATH  MathSciNet  Google Scholar 

  3. P. K. Agarwal and M. Sharir, Red-blue intersection detection algorithms, with applications to motion planning and collision detection, SIAM J. Comput., 19 (1990), 297–321.

    Article  MATH  MathSciNet  Google Scholar 

  4. P. K. Agarwal and M. Sharir, Ray shooting amidst convex polygons in 2D, J. Algorithms, 21 (1996), 508–519.

    Article  MATH  MathSciNet  Google Scholar 

  5. I. Balaban, An optimal algorithm for finding segment intersections, Proc. 11th Annu. ACM Sympos. Comput. Geom., 1995, pp. 211–219.

    Google Scholar 

  6. J. Basch, L. J. Guibas, and G. Ramkumar, Sweeping lines and line segments with a heap, Proc. 13th Annu. ACM Sympos. Comput. Geom., 1997, pp. 469–472.

    Google Scholar 

  7. J. L. Bentley and T. A. Ottmann, Algorithms for reporting and counting geometric intersections, IEEE Trans. Comput., C-28 (1979), 643–647.

    Article  Google Scholar 

  8. G. Brodal and R. Jacob, Dynamic planar convex hull with optimal query time and o(logn\loglogn) update time, Proc. 7th Scand. Workshop Algorithm Theory, 2000, pp. 57–70.

    Google Scholar 

  9. B. Chazelle, Cutting hyperplanes for divide-and-conquer, Discrete Comput. Geom., 9 (1993), 145–158.

    Article  MATH  MathSciNet  Google Scholar 

  10. B. Chazelle and L. Guibas, Fractional cascading: I. A data structuring technique, Algorithmica, 1 (1986), 133–162.

    Article  MATH  MathSciNet  Google Scholar 

  11. B. Chazelle, L. Guibas, and D. T. Lee, The power of geometric duality, BIT, 25 (1985), 76–90.

    Article  MATH  MathSciNet  Google Scholar 

  12. B. Chzelle and H. Edelsbrunner, An optimal algorithm for intersecting line segments in the plane, J. ACM, 39 (1992), 1–54.

    Article  Google Scholar 

  13. B. Chzelle, H. Edelsbrunner, L. Guibas, and M. Sharir, Algorithms for bichromatic line segment problems and polyhedral terrains, Algorithmica, 11 (1994), 116–132.

    Article  MathSciNet  Google Scholar 

  14. K. L. Clarkson and P. Shor, Applications of random sampling in computational geometry, II, Discrete Comput. Geom., 4 (1989), 387–421.

    Article  MATH  MathSciNet  Google Scholar 

  15. U. Finke and K. Hinrichs, Overlaying simply connected planar subdivisions in linear time, Proc. 11th Annu. ACM Sympos. Comput. Geom., 1995, pp. 119–126.

    Google Scholar 

  16. P. Gupta, R. Janardan, and M. Smid, Efficient algorithms for counting and reporting pairwise intersections between convex polygons, Inform. Process. Lett., 69 (1999), 7–13.

    Article  MathSciNet  Google Scholar 

  17. S. Har-Peled and M. Sharir, On-line point location in planar arrangements and its applications, Proc. 12th ACM-SIAM Sympos. Discrete Algorithms, 2001, pp. 57–66.

    Google Scholar 

  18. J. Matousek, Range searching with efficient hierarchical cuttings, Discrete Comput. Geom., 10 (1993), 157–182.

    Article  MATH  MathSciNet  Google Scholar 

  19. K. Mulmuley, A fast planar partition algorithm, I, J. Symbolic Comput., 10 (1990), 253–280.

    Article  MATH  MathSciNet  Google Scholar 

  20. N. Sarnak and R. E. Tarjan, Planar point location using persistent search trees, Commun. ACM, 29 (1986), 669–679.

    Article  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Center for Geometric Computing, Department of Computer Science, Duke University, Durham, NC, 27708, USA

    Pankaj K. Agarwal

  2. Institute of Information and Computing Sciences, Utrecht University, P.O.Box 80.089, 3508, TB Utrecht, The Netherlands

    Mark de Berg & Mark H. Overmars

  3. Department of Computer Science, DCL 2111, University of Illinois, 1304 West Springfield Ave., Urbana, IL, 61801, USA

    Sariel Har-Peled

  4. School of Computer Science, Tel Aviv University, Tel Aviv, 69978, Israel

    Micha Sharir

  5. Courant Institute of Mathematical Sciences, New York University, New York, NY, 10012, USA

    Micha Sharir

  6. Institut für Informatik, Westfälische Wilhelms-Universität Münster, 48149, Münster, Germany

    Jan Vahrenhold

Authors
  1. Pankaj K. Agarwal
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Mark de Berg
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Sariel Har-Peled
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Mark H. Overmars
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Micha Sharir
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Jan Vahrenhold
    View author publications

    You can also search for this author in PubMed Google Scholar

Editor information

Editors and Affiliations

  1. School of Computer Science, Carleton University, 1125 Colonel By Drive, Ottawa, Candada, K1S 5B6

    Frank Dehne  & Jörg-Rüdiger Sack  & 

  2. Center for Geometric Computing, Brown University, Providence, RI, 02912-1910, USA

    Roberto Tamassia

Rights and permissions

Reprints and permissions

Copyright information

© 2001 Springer-Verlag Berlin Heidelberg

About this paper

Cite this paper

Agarwal, P.K., de Berg, M., Har-Peled, S., Overmars, M.H., Sharir, M., Vahrenhold, J. (2001). Reporting Intersecting Pairs of Polytopes in Two and Three Dimensions. In: Dehne, F., Sack, JR., Tamassia, R. (eds) Algorithms and Data Structures. WADS 2001. Lecture Notes in Computer Science, vol 2125. Springer, Berlin, Heidelberg. https://doi.org/10.1007/3-540-44634-6_12

Download citation

  • DOI: https://doi.org/10.1007/3-540-44634-6_12

  • Published:

  • Publisher Name: Springer, Berlin, Heidelberg

  • Print ISBN: 978-3-540-42423-9

  • Online ISBN: 978-3-540-44634-7

  • eBook Packages: Springer Book Archive

Publish with us

Policies and ethics