Abstract
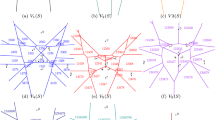
In this paper we discuss the kinetic maintenance of the Euclidean Voronoi diagram and its dual, the Delaunay triangulation, for a set of moving disks. The most important aspect in our approach is that we can maintain the Voronoi diagram even in the case of intersecting disks. We achieve that by augmenting the Delaunay triangulation with some edges associated with the disks that do not contribute to the Voronoi diagram. Using the augmented Delaunay triangulation of the set of disks as the underlying structure, we discuss how to maintain, as the disks move, (1) the closest pair, (2) the connectivity of the set of disks and (3) in the case of non-intersecting disks, the near neighbors of a disk.
Supported by NSF grant CCR-9910633.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
J. Basch, L. J. Guibas, and J. Hershberger. Data structures for mobile data. J. Algorithms, 1:1–28, 1999.
M. Gavrilova and J. Rokne. Swap conditions for dynamic Voronoi diagrams for circles and line segments. CAGD, 16:89–106, 1999.
L. J. Guibas, J. Hershberger, S. Suri, and L. Zhang. Kinetic connectivity for unit disks. In Proc. 16th ACM Symp. on Computat. Geom., pages 331–339, 2000.
L. J. Guibas, J. S. B. Mitchell, and T. Roos. Voronoi diagrams of moving points in the plane. In G. Schmidt and R. Berghammer, editors, Proc. 17th International Workshop on Graph-Theoretic Concepts in Computer Science, volume 570 of LNCS, pages 113–125. Springer, 1991.
L. J. Guibas, J. Snoeyink, and L. Zhang. Compact Voronoi diagrams for moving convex polygons. In Magnús M. Halldórsson, editor, Proc. 7th SWAT, volume 1851 of LNCS, pages 339–352. Springer, 2000.
L. J. Guibas and L. Zhang. Euclidean proximity and power diagram. In Proc. 10th CCCG, 1998.
J. Holm, K. de Lichtenberg, and M. Thorup. Poly-logarithmic deterministic fully-dynamic algorithms for connectivity, minimum spanning tree, 2-edge, and bicon-nectivity. In Proc. 30th ACM STOC, pages 79–89, 1998.
H. Imai, M. Iri, and K. Murota. Voronoi diagram in the Laguerre geometry and its applications. SIAM J. Comput., 14(1):93–105, 1985.
M. I. Karavelas and L. J. Guibas. Static and kinetic geometric spanners with applications. In Proc. 12th ACM-SIAM SODA, pages 168–176, 2001.
J.-C. Latombe. Robot Motion Planning. Kluwer Academic Publishers, Boston, 1991.
M. C. Lin and J. F. Canny. Efficient algorithms for incremental distance computation. In Proc. IEEE Intern. Conf. Robot. Autom., volume 2, pages 1008–1014, 1991.
M. Sharir. Intersection and closest-pair problems for a set of planar discs. SIAM J. of Comput., 14(2):448–468, May 1985.
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2001 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Karavelas, M.I. (2001). Voronoi Diagrams for Moving Disks and Applications. In: Dehne, F., Sack, JR., Tamassia, R. (eds) Algorithms and Data Structures. WADS 2001. Lecture Notes in Computer Science, vol 2125. Springer, Berlin, Heidelberg. https://doi.org/10.1007/3-540-44634-6_7
Download citation
DOI: https://doi.org/10.1007/3-540-44634-6_7
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-42423-9
Online ISBN: 978-3-540-44634-7
eBook Packages: Springer Book Archive