Abstract
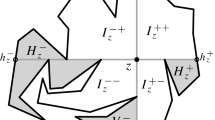
Let N be a set of n points in convex position in ∝3. The farthest-point Voronoi diagram of N partitions ∝3 into n convex cells. We consider the intersection G(N) of the diagram with the boundary of the convex hull of N. We give an algorithm that computes an implicit representation of G(N) in expected O(n log2 n) time. More precisely, we compute the combinatorial structure of G(N), the coordinates of its vertices, and the equation of the plane de?ning each edge of G(N). The algorithm allows us to solve the all-pairs farthest neighbor problem for N in expected time O(n log2 n), and to perform farthest-neighbor queries on N in O(log2 n) time with high probability. This can be applied to find a Euclidean maximum spanning tree and a diameter 2-clustering of N in expected O(n log4 n) time.
This research was partially supported by the Hong Kong Research Grants Council.Part of it was done when the first two authors were at HKUST. The second author’s research was supported by grant No. 98-0102-07-01-3 from KOSEF and also supported by BK21 Research Professor Program at KAIST.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
Pankaj K. Agarwal, J. Matouísek, and Subhash Suri Farthest neighbors, maximum spanning trees and related problems in higher dimensions. Comput. Geom. Theory Appl., 1(4):189–201, 1992.
A. Aggarwal and D. Kravets A linear time algorithm for finding all farthest neighbors in a convex polygon. Information Processing letters, 31(1):17–20, 1989.
Sergei N. Bespamyatnikh An efficient algorithm for the three-dimensional diameter problem. In Proc. 9th ACM-SIAM Sympos. Discrete Algorithms, pages 137–146, 1998.
K.L. Clarkson and P.W. Shor Applications of random sampling in computational geometry, II. Discrete Comput. Geom., 4:387–421, 1989.
K. Mulmuley Computational Geometry: An Introduction Through Randomized Algorithms. Prentice Hall, Englewood Cliffs, NJ, 1994.
F.P. Preparata and M.I. Shamos Computational Geometry: An Introduction. Springer-Verlag, New York, NY, 1985.
E. Ramos Construction of 1-d lower envelopes and applications. In Proc. 13th Annu. ACM Sympos. Comput. Geom., pp. 57–66, 1997.
E. Ramos An optimal deterministic algorithm for computing the diameter of a 3-d point set. In Proc. 16th Annu. ACM Sympos. Comput. Geom., page to appear, 2000.
P.M. Vaidya An O(n log n) algorithm for the all-nearest-neighbors problem. Discrete Comput. Geom., 4:101–115, 1989.
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2001 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Cheong, O., Shin, CS., Vigneron, A. (2001). Computing Farthest Neighbors on a Convex Polytope. In: Wang, J. (eds) Computing and Combinatorics. COCOON 2001. Lecture Notes in Computer Science, vol 2108. Springer, Berlin, Heidelberg. https://doi.org/10.1007/3-540-44679-6_18
Download citation
DOI: https://doi.org/10.1007/3-540-44679-6_18
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-42494-9
Online ISBN: 978-3-540-44679-8
eBook Packages: Springer Book Archive