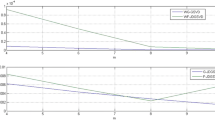
Abstract
In this paper the solution of an inverse singular value problem is considered. First the decomposition of a real square matrix A = UΣV is introduced, where U and V are real square matrices orthogonal with respect to a particular inner product defined through a real diagonal matrix G of order n having all the elements equal to ±1, and Σ is a real diagonal matrix with nonnegative elements, called G-singular values. When G is the identity matrix this decomposition is the usual SVD and Σ is the diagonal matrix of singular values. Given a set σ1, ..., σn of n real positive numbers we consider the problem to find a real matrix A having them as G-singular values. Neglecting theoretical aspects of the problem, we discuss only an algorithmic issue, trying to apply a Newton type algorithm already considered for the usual inverse singular value problem.
Chapter PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
References
Bojanczyk A.W., Onn R., Steinhardt A.O.: Existence of The Hyperbolic Singular Value Decomposition. Linear Algebra Appl. 185 (1993) 21–30
Chu M.T.: Numerical methods for inverse singular value problems. SIAM J. Numer. Anal. 29(3) (1992) 885–903
Chu M.T.: Inverse eigenvalue problems. SIAM Rev. 40(1) (1998) 1–39
Di Lena G., Piazza G., Politi T.: An algorithm for the computation of the G-singular values of a matrix. Manuscript.
Friedland S.: Inverse eigenvalue problems. Linear Algebra Appl. 17 (1977) 15–51
Lopez L., Politi T.: Applications of the Cayley Approach in the Numerical Solution of Matrix Differential Systems on Quadratic Groups. Appl. Num. Math. 36 (2001) 35–55
Onn R., Steinhardt A.O., Bojanczyk A.W.: The Hyperbolic Singular Value Decomposition and applications. IEEE Trans. Sign. Proc. 39(7) (1991) 1575–1588
Rader C.M., Steinhardt A.O.: Hyperbolic Householder Transforms. SIAM J. Matrix Anal. 9 (1988) 269–290
Renardy M.: Singular values decomposition in Minkowski space. Linear Algebra Appl. 236 (1996) 53–58
Xing Z.: On the deterministic and nondeterministic Mueller matrix. J. ModernOpt. 39 (1992) 461–484
Zha H.: A note on the existence of The Hyperbolic Singular Value Decomposition. Linear Algebra Appl. 240 (1996) 199–205
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2003 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Politi, T. (2003). A Discrete Approach for the Inverse Singular Value Problem in Some Quadratic Group. In: Sloot, P.M.A., Abramson, D., Bogdanov, A.V., Gorbachev, Y.E., Dongarra, J.J., Zomaya, A.Y. (eds) Computational Science — ICCS 2003. ICCS 2003. Lecture Notes in Computer Science, vol 2658. Springer, Berlin, Heidelberg. https://doi.org/10.1007/3-540-44862-4_14
Download citation
DOI: https://doi.org/10.1007/3-540-44862-4_14
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-40195-7
Online ISBN: 978-3-540-44862-4
eBook Packages: Springer Book Archive