Skip to main content
SpringerLink
Log in

Approximating Fuzzy Control Strategies via CRI

  • Conference paper
  • First Online:
Fuzzy Sets and Systems — IFSA 2003 (IFSA 2003)

Part of the book series: Lecture Notes in Computer Science ((LNAI,volume 2715))

Included in the following conference series:

  • 1255 Accesses

Abstract

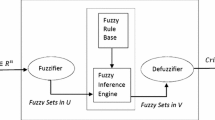
We start from the observation that Zadeh’s compositional rule of inference (CRI) is a strategy to determine approximately a roughly given control function.

From this point of view the problem to solve a system of fuzzy relation equations also becomes the problem to determine approximately such a control strategy. This gives a natural interpretation for approximate solutions of unsolvable systems of relation equations.

Therefore we discuss and generalize some approaches and results about approximate solutions of systems of relation equations.

Finally we discuss here how a choice of the t-norm which is involved in the sup-t-composition modifies the solvability behavior.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution
Chapter
USD 29.95
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever
eBook
USD 84.99
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever
Softcover Book
USD 109.99
Price excludes VAT (USA)
  • Compact, lightweight edition
  • Dispatched in 3 to 5 business days
  • Free shipping worldwide - see info

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Preview

Unable to display preview. Download preview PDF.

Unable to display preview. Download preview PDF.

References

  1. Gottwald, S. (1993): Fuzzy Sets and Fuzzy Logic. The Foundations of Application — from a Mathematical Point of View. Vieweg: Braunschweig/Wiesbaden and Teknea: Toulouse.

    Google Scholar 

  2. Gottwald, S. (2001): A Treatise on Many-Valued Logics. Research Stud. Press, Baldock.

    MATH  Google Scholar 

  3. Gottwald, S., Novak, V. and I. Perfilieva (2002): Fuzzy control and t-normbased fuzzy logic. Some recent results. In: Proc. 9th Internat. Conf. IPMU 2002, vol. 2, ESIA — Université de Savoie: Annecy 2002, 1087–1094.

    Google Scholar 

  4. Klir, G. and B. Yuan (1994): Approximate solutions of systems of fuzzy relation equations. In: FUZZ-IEEE’ 94. Proc. 3rd Internat. Conf. Fuzzy Systems, June 26–29, 1994, Orlando/FL, 1452–1457.

    Google Scholar 

  5. Klir, G. and B. Yuan (1995): Fuzzy Sets and Fuzzy Logic. Theory and Applications. Prentice Hall: Upper Saddle River.

    Google Scholar 

  6. Klawonn, F. (2001): Fuzzy points, fuzzy relations and fuzzy functions. In: Discovering the World with Fuzzy Logic (V. Novák, I. Perfilieva eds.) Advances in Soft Computing, Physica-Verlag: Heidelberg 2000, 431–453.

    Google Scholar 

  7. Mamdani, A. and S. Assilian (1975): An experiment in linguistic synthesis with a fuzzy logic controller. Internat. J. Man-Machine Studies7, 1–13.

    Article  MATH  Google Scholar 

  8. Novák, V., Perfilieva, I. and J. Mockor (1999): Mathematical Principles of Fuzzy Logic. Kluwer Acad. Publ., Boston.

    MATH  Google Scholar 

  9. Perfilieva, I. and S. Gottwald (200x): Solvability and approximate solvability of fuzzy relation equations (submitted).

    Google Scholar 

  10. Sanchez, E. (1976): Resolution of composite fuzzy relation equations. Information and Control30, 38–48.

    Article  MathSciNet  MATH  Google Scholar 

  11. Wu Wangming (1986): Fuzzy reasoning and fuzzy relation equations, Fuzzy Sets Systems20, 67–78.

    Article  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Institute for Logic, Leipzig University, Leipzig, Germany

    Siegfried Gottwald

  2. IRAFM, Ostrava University, Ostrava, Czech Republic

    Vilem Novák & Irina Perfilieva

Authors
  1. Siegfried Gottwald
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Vilem Novák
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Irina Perfilieva
    View author publications

    You can also search for this author in PubMed Google Scholar

Editor information

Editors and Affiliations

  1. Department of Industrial Engineering, Boğaziçi University, 34342, Bebek, Istanbul, Turkey

    Taner Bilgiç

  2. Dept. of Applied Mathematics, Biometrics and Process Control, Ghent University, Coupure links 653, 9000, Gent, Belgium

    Bernard De Baets

  3. Department of Electrical and Electronics Engineering, Boğaziçi University, 34342, Bebek, Istanbul, Turkey

    Okyay Kaynak

Rights and permissions

Reprints and permissions

Copyright information

© 2003 Springer-Verlag Berlin Heidelberg

About this paper

Cite this paper

Gottwald, S., Novák, V., Perfilieva, I. (2003). Approximating Fuzzy Control Strategies via CRI. In: Bilgiç, T., De Baets, B., Kaynak, O. (eds) Fuzzy Sets and Systems — IFSA 2003. IFSA 2003. Lecture Notes in Computer Science, vol 2715. Springer, Berlin, Heidelberg. https://doi.org/10.1007/3-540-44967-1_24

Download citation

  • DOI: https://doi.org/10.1007/3-540-44967-1_24

  • Published:

  • Publisher Name: Springer, Berlin, Heidelberg

  • Print ISBN: 978-3-540-40383-8

  • Online ISBN: 978-3-540-44967-6

  • eBook Packages: Springer Book Archive

Publish with us

Policies and ethics

Search

Navigation