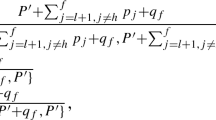Skip to main content
Springer Nature Link
Log in

Improved Competitive Algorithms for Online Scheduling with Partial Job Values

  • Conference paper
  • First Online:
Computing and Combinatorics (COCOON 2003)

Part of the book series: Lecture Notes in Computer Science ((LNCS,volume 2697))

Included in the following conference series:

Abstract

This paper considers an online scheduling problem arising from Quality-of-Service (QoS) applications. We are required to schedule a set of jobs, each with release time, deadline, processing time and weight. The objective is to maximize the total value obtained for scheduling the jobs. Unlike the traditional model of this scheduling problem, in our model unfinished jobs also get partial values proportional to their amounts processed.

We give a new non-timesharing algorithm GAP for this problem for bounded m, where m is the number of concurrent jobs or the number of weight classes. The competitive ratio is improved from 2 to 1.618 (golden ratio) which is optimal for m = 2, and when applied to cases with m > 2 it still gives a competitive ratio better than 2, e.g. 1.755 when m = 3. We also give a new study of the problem in the multiprocessor setting, giving an upper bound of 2 and a lower bound of 1.25 for the competitiveness. Finally, we consider resource augmentation and show that O(log α) speedup or extra processors is sufficient to achieve optimality, where α is the importance ratio. We also give a tradeoff result between competitiveness and the amount of extra resources.

This work is supported by an RGC research grant.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Chapter
USD 29.95
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Preview

Unable to display preview. Download preview PDF.

Unable to display preview. Download preview PDF.

Similar content being viewed by others

References

  1. S. Baruah, G. Koren, D. Mao, B. Mishra, A. Raghunathan, L. Rosier, D. Shasha and F. Wang, On the Competitiveness of On-line Real-time Task Scheduling, Real-Time Systems 4, 125–144, 1992.

    Article  MATH  Google Scholar 

  2. A. Borodin and R. El-Yaniv, Online Computation and Competitive Analysis, Cambridge University Press, New York, 1998.

    MATH  Google Scholar 

  3. E. Chang and C. Yap, Competitive Online Scheduling with Level of Service, Proceedings of 7th Annual International Computing and Combinatorics Conference, 453–462, 2001.

    Google Scholar 

  4. F. Y. L. Chin and S. P. Y. Fung, Online Scheduling with Partial Job Values and Bounded Importance Ratio, Proceedings of International Computer Symposium, 787–794, 2002.

    Google Scholar 

  5. F. Y. L. Chin and S. P. Y. Fung, Online Scheduling with Partial Job Values: Does Timesharing or Randomization Help? to appear in Algorithmica.

    Google Scholar 

  6. M. Chrobak, L. Epstein, J. Noga, J. Sgall, R. van Stee, T. Tichý and N. Vakhania, Preemptive Scheduling in Overloaded Systems, preliminary version appeared in Proceedings of 29th International Colloqium on Automata, Languages and Programming, 800–811, 2002.

    Google Scholar 

  7. B. Kalyanasunaram and K. Pruhs, Speed is as Powerful as Clairvoyance, Journal of the ACM 47(4), 617–643, 2000.

    Article  MathSciNet  Google Scholar 

  8. C.-Y. Koo, T.-W. Lam, T.-W. Ngan and K.-K. To, Extra Processors versus Future Information in Optimal Deadline Scheduling, Proceedings of 15th ACM Symposium on Parallelism in Algorithms and Architectures, 133–142, 2002.

    Google Scholar 

  9. G. Koren and D. Shasha, D over: An Optimal On-line Scheduling Algorithm for Overloaded Uniprocessor Real-time Systems, SIAM Journal on Computing 24, 318–339, 1995.

    Article  MATH  MathSciNet  Google Scholar 

  10. T.-W. Lam and K.-K. To, Performance Guarantee for Online Deadline Scheduling in the Presence of Overload, Proceedings of 12th Annual ACM-SIAM Symposium on Discrete Algorithms, 755–764, 2001.

    Google Scholar 

  11. J. W. S. Liu, K.-J. Lin, W.-K. Shih, A. C.-S. Yu, J.-Y. Chung and W. Zhao, Algorithms for Scheduling Imprecise Computations, IEEE Computer 24(5), 58–68, 1991.

    Google Scholar 

  12. C. A. Philips, C. Stein, E. Torng and J. Wein, Optimal Time-critical Scheduling via Resource Augmentation, Proceedings of 29th Annual ACM Symposium on Theory of Computing, 140–149, 1997.

    Google Scholar 

  13. D. Sleator and R. Tarjan, Amortized Efficiency of List Update and Paging Rules, Communications of the ACM 28(2), 202–208, 1985.

    Article  MathSciNet  Google Scholar 

  14. A. C.-C. Yao, Probabilistic Computations: Toward a Unified Measure of Complexity, Proceedings of 18th IEEE Symposium on Foundations of Computer Science, 222–227, 1977.

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Computer Science and Information Systems, The University of Hong Kong, Hong Kong

    Francis Y. L. Chin & Stanley P. Y. Fung

Authors
  1. Francis Y. L. Chin
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Stanley P. Y. Fung
    View author publications

    You can also search for this author in PubMed Google Scholar

Editor information

Editors and Affiliations

  1. Department of Computer Science, University of Texas at Austin, One University Station, C0500, Austin, TX, 78712, USA

    Tandy Warnow

  2. Department of Computer Science, Montana State University, EPS 357, Bozeman, MT, 59717, USA

    Binhai Zhu

Rights and permissions

Reprints and permissions

Copyright information

© 2003 Springer-Verlag Berlin Heidelberg

About this paper

Cite this paper

Chin, F.Y.L., Fung, S.P.Y. (2003). Improved Competitive Algorithms for Online Scheduling with Partial Job Values. In: Warnow, T., Zhu, B. (eds) Computing and Combinatorics. COCOON 2003. Lecture Notes in Computer Science, vol 2697. Springer, Berlin, Heidelberg. https://doi.org/10.1007/3-540-45071-8_43

Download citation

  • DOI: https://doi.org/10.1007/3-540-45071-8_43

  • Published:

  • Publisher Name: Springer, Berlin, Heidelberg

  • Print ISBN: 978-3-540-40534-4

  • Online ISBN: 978-3-540-45071-9

  • eBook Packages: Springer Book Archive

Publish with us

Policies and ethics