Abstract
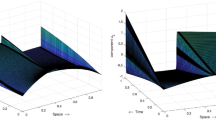
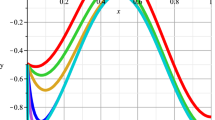
The central difference scheme for reaction-diffusion problems, when fitted Shishkin type meshes are used, gives uniformly convergent methods of almost second order. In this work, we construct HOC (High Order Compact) compact monotone finite difference schemes, defined on a priori Shishkin meshes, uniformly convergent with respect the diffusion parameter ∈, which have order three and four except for a logarithmic factor. We show some numerical experiments which support the theoretical results.
This research was supported by the project DGES-PB97-1013
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
J. L. Gracia, Esquemas de orden superior para problemas de convección-difusión y reacción-difusión lineales, Ph. Thesis, University of Zaragoza, (1999) (in spanish).
A. F. Hegarty, J. J. H. Miller, E. O’Riordan, G. I. Shishkin, Special numerical methods for convection-dominated laminar flows at arbitrary Reynolds number, East-West J. Numer. Math. 2 (1994) 65–74.
J. J. H. Miller, E. O’Riordan, G. I. Shishkin, Fitted numerical methods for singular perturbation problems. Error estimates in the maximum norm for linear problems in one and two dimensions, World Scientific, (1996).
H. G. Roos, M. Stynes, L. Tobiska, Numerical methods for singularly perturbed differential equations, Springer-Verlag, (1996).
A. A. Samarski, V. B. Andréiev, Métodos en diferencias para las ecuaciones elípticas, Mir, Moscú, (1979).
G. I. Shishkin, Discrete approximation of singularly perturbed elliptic and parabolic equations, Russian Academic of Sciences. Ural Section. Ekaterinburg, (1992).
G. I. Shishkin, Approximation of solutions of singularly perturbed boundary value problems with a parabolic boundary layer, USSR Comput. Maths. Maths. Phys. 29 (1989) 1–10.
W. F. Spotz, High-order compact finite difference schemes for computational mechanics, Ph. D. Thesis, University of Texas at Austin, (1995).
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2001 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Gracia, J.L., Lisbona, F., Clavero, C. (2001). High Order ε-Uniform Methods for Singularly Perturbed Reaction-Diffusion Problems. In: Vulkov, L., Yalamov, P., Waśniewski, J. (eds) Numerical Analysis and Its Applications. NAA 2000. Lecture Notes in Computer Science, vol 1988. Springer, Berlin, Heidelberg. https://doi.org/10.1007/3-540-45262-1_41
Download citation
DOI: https://doi.org/10.1007/3-540-45262-1_41
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-41814-6
Online ISBN: 978-3-540-45262-1
eBook Packages: Springer Book Archive