Skip to main content
SpringerLink
Log in
Book cover

International Conference on Numerical Analysis and Its Applications

NAA 2000: Numerical Analysis and Its Applications pp 377–384Cite as

Positive Definite Solutions of the Equation X + A*X -n A=I

  • Conference paper
  • First Online:

Part of the book series: Lecture Notes in Computer Science ((LNCS,volume 1988))

Abstract

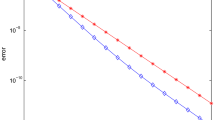
The general nonlinear matrix equation X + A*X -n A I is discussed (n is a positive integer). Some necessary and sufficient conditions for existence a solution are given. Two methods for iterative computing a positive definite solution are investigated. Numerical experiments to illustrate the performance of the methods are reported.

This is a preview of subscription content, log in via an institution.

Chapter
USD   29.95
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever
eBook
USD   109.00
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever
Softcover Book
USD   139.99
Price excludes VAT (USA)
  • Compact, lightweight edition
  • Dispatched in 3 to 5 business days
  • Free shipping worldwide - see info

Tax calculation will be finalised at checkout

Purchases are for personal use only

Learn about institutional subscriptions

Preview

Unable to display preview. Download preview PDF.

Unable to display preview. Download preview PDF.

References

  1. Engwerda, J., Ran, A., Rijkeboer, A.: Necessary and Sufficient Conditions for the Existence of a Positive Definite Solution of the Matrix EquationX+A * X -1 A = Q. Linear Algebra Appl. 186 (1993) 255–275

    Article  MATH  MathSciNet  Google Scholar 

  2. Engwerda, J.: On the Existence of a Positive Definite Solution of the Matrix Equation X+A T X -1 A = I. Linear Algebra Appl. 194 (1993) 91–108

    Article  MATH  MathSciNet  Google Scholar 

  3. El-Sayed, S., Ran, A.: On an Method for Solving a Class of Nonlinear Matrix Equations. SIAM J. on Matrix Analysis /to appear/

    Google Scholar 

  4. Golub, G., van Loan C.: Matrix Computations, John Hopkins, Baltimore (1989)

    MATH  Google Scholar 

  5. Guo, C., Lancaster, P.: Iterative Solution of Two Matrix Equations. Mathematics of Computation 68 (1999) 1589–1603

    Article  MATH  MathSciNet  Google Scholar 

  6. Ivanov, I., El-Sayed, S.: Properties of Positive Definite Solution of the Equation X+A * X -2 A = I. Linear Algebra And Appl. 279 (1998) 303–316

    Article  MATH  MathSciNet  Google Scholar 

  7. Kwong, M.: Some Results on Matrix Monotone Functions. Linear Algebra And Appl. 118 (1989) 129–153

    Article  MATH  MathSciNet  Google Scholar 

  8. Zhan, X.: Computing the Extremal positive definite solution of a Matrix Equation. SIAM J. Sci. Comput. 247 (1996) 337–345

    MATH  MathSciNet  Google Scholar 

  9. Zhan, X., Xie, J.: On the Matrix Equation X+A T X -1 A = Q. Linear Algebra And Appl. 247 (1996) 337–345

    Article  MATH  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Laboratory Mathematical Modelling, Shoumen University, 9712, Shoumen, Bulgaria

    Vejdi Hassanov & Ivan Ivanov

Authors
  1. Vejdi Hassanov
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Ivan Ivanov
    View author publications

    You can also search for this author in PubMed Google Scholar

Editor information

Editors and Affiliations

  1. Department of Computer Science, University of Rousse, 7000, Rousse, Bulgaria

    Lubin Vulkov  & Plamen Yalamov  & 

  2. UNI-C,Danish Computing Center for Research and Education, DTU,Building 304, 2800, Lyngby, Denmark

    Jerzy Waśniewski

Rights and permissions

Reprints and permissions

Copyright information

© 2001 Springer-Verlag Berlin Heidelberg

About this paper

Cite this paper

Hassanov, V., Ivanov, I. (2001). Positive Definite Solutions of the Equation X + A*X -n A=I . In: Vulkov, L., Yalamov, P., Waśniewski, J. (eds) Numerical Analysis and Its Applications. NAA 2000. Lecture Notes in Computer Science, vol 1988. Springer, Berlin, Heidelberg. https://doi.org/10.1007/3-540-45262-1_44

Download citation

  • DOI: https://doi.org/10.1007/3-540-45262-1_44

  • Published:

  • Publisher Name: Springer, Berlin, Heidelberg

  • Print ISBN: 978-3-540-41814-6

  • Online ISBN: 978-3-540-45262-1

  • eBook Packages: Springer Book Archive

Publish with us

Policies and ethics

Search

Navigation