Abstract
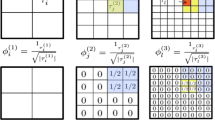
In [7], a large class of bi-variate finite orthogonal wavelet filters was constructed. In this paper, we propose a more general expression of the filter bank with linear phase which is called standard method. Beside this, a non-standard method is also presented. A interesting example is also given. By using this non-separable wavelet filter bank, we present a novel method of segmenting a image into two parts: one part is texture with special property and another part is image of piecewise smooth in some sense.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
I. Daubechies, Ten Lectures on Wavelets, CBMS, 61,SIAM, Philadelphia, 1992.
Wenjie He and Mingjun Lai, Construction of Bivariate Compactly supported Biorthogonal Box Spline Wavelets with Arbitrarily High Regularities, Applied Comput. Harmonic Analysis, 6(1999) 53–74.
Wenjie He and Mingjun Lai, Examples of Bivariate Nonseparable Compactly Supported Orthonormal Continuous Wavelets, Wavelet Applications in Signal and Image Processing IV, Proceedings of SPIE, 3169(1997) 303–314.
J. Kovacevic and M. Vetterli, Nonseparable multidimensional perfect reconstruction filter banks and wavelet bases for R n, IEEE Tran. on Information Theory, 38, 2(1992) 533–555.
S. Mallat, Review of Multifrequency Channel Decomposition of Images and Wavelet Models, Technical report 412, Robotics Report 178, New York Univ., (1988).
Y. Meyer, Principe d’incertitude, Bases hilbertiennes et algebres d’oper-ateurs, Seminaire Bourbaki 662, 1985–86, Asterisque (Societe Mathematique de France).
Silong Peng, Construction of Two Dimensional Compactly Supported Orthogonal Wavelet Filters with Linear Phase, (to appear in ACTA Mathematica Sinica), (1999).
Silong Peng, Characterization of Separable Bivariate Orthonormal Compactly Supported Wavelet Basis, (to appear in ACTA Mathematica Sinica), (1999).
Silong Peng, N dimensional Compactly Supported Orthogonal Wavelet Filters, (to appear in J. of Computational Mathematics), (1999).
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2001 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Chen, H., Peng, S. (2001). Construction of Finite Non-separable Orthogonal Filter Banks with Linear Phase and Its Application in Image Segmentation. In: Tang, Y.Y., Yuen, P.C., Li, Ch., Wickerhauser, V. (eds) Wavelet Analysis and Its Applications. WAA 2001. Lecture Notes in Computer Science, vol 2251. Springer, Berlin, Heidelberg. https://doi.org/10.1007/3-540-45333-4_28
Download citation
DOI: https://doi.org/10.1007/3-540-45333-4_28
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-43034-6
Online ISBN: 978-3-540-45333-8
eBook Packages: Springer Book Archive