Abstract
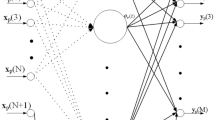
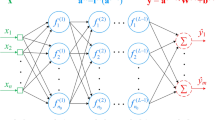
We introduce a Forward Backward and Model Selection algorithm (FBMS) for constructing a hybrid regression network of radial and perceptron hidden units. The algorithm determines whether a radial or a perceptron unit is required at a given region of input space. Given an error target, the algorithm also determines the number of hidden units. Then the algorithm uses model selection criteria and prunes unnecessary weights. This results in a final architecture which is often much smaller than a RBF network or a MLP. Results for various data sizes on the Pumadyn data indicate that the resulting architecture competes and often outperform best known results for this data set.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
L. Breiman, J. H. Friedman, R. A. Olshen, and C. J. Stone. Classification and Regression Trees. The Wadsworth Statistics/Probability Series, Belmont, CA, 1984.
C.E. Rasmussen, R.M. Neal, G.E. Hinton, D. Van Camp, Z. Ghahrman M. Revow, R. Kustra, and R. Tibshirani. The delve manual. 1996.
S. Cohen and N. Intrator. Automatic model selection of ridge and radial functions. In Second International workshop on Multiple Classifier Systems, 2001.
S. Cohen and N. Intrator. A hybrid projection based and radial basis function architecture: Initial values and global optimization. To appear in Special issue of PAA on Fusion of Multiple Classifiers, 2001.
D. L. Donoho and I. M. Johnstone. Projection-based approximation and a duality with kernel methods. Annals of Statistics, 17:58–106, 1989.
G.W. Flake. Square unit augmented, radially extended, multilayer percpetrons. In G. B. Orr and K. Müller, editors, Neural Networks: Tricks of the Trade, pages 145–163. Springer, 1998.
J. H. Friedman. Mutltivariate adaptive regression splines. The Annals of Statistics, 19:1–141, 1991.
B. Hassibi and D. G. Stork. Second order derivatives for network pruning: Optimal brain surgeon. In C. L. Giles, S. J. Hanson, and J. D. Cowan, editors, Advances in Neural Information Processing Systems, volume 5. Morgan Kaufmann, San Mateo, CA, 1993.
R. A. Jacobs, M. I. Jordan, S. J. Nowlan, and G. E. Hinton. Adaptive mixtures of local experts. Neural Computation, 3(1):79–87, 1991.
N. Sugie K. Suzuki, I. Horiba. A simple neural network algorithm with application to filter synthesis. Neural Processing Letters, Kluwer Academic Publishers, Netherlands, 13:43–53, 2001.
R. E. Kass and A. E. Raftery. Bayes factors. Journal of The American Statistical Association, 90:773–795, 1995.
Y.C. Lee, G. Doolen, H.H. Chen, G.Z. Sun, T. Maxwell, H.Y. Lee, and C.L. Giles. Machine learning using higher order correlation networks. Physica D, pages 22-D: 276–306, 1986.
R. M. Neal. Bayesian Learning for Neural Networks. Springer, New York, 1996.
S. J. Nowlan. Soft competitive adaptation: Neural network learning algorithms basd on fitting statistical mixtures. Ph.D. dissertation, Carnegie Mellon University, 1991.
A. Papoulis. Probbaility, Random Variables, and Stochastic Process, volume 1. McGRAW-HILL, New York, third edition, 1991.
D. G. Stork R. O. Duda, P. E. Hart. Pattern Classification. John Wiley Sons, INC., New York, 2001.
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2002 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Cohen, S., Intrator, N. (2002). Forward and Backward Selection in Regression Hybrid Network. In: Roli, F., Kittler, J. (eds) Multiple Classifier Systems. MCS 2002. Lecture Notes in Computer Science, vol 2364. Springer, Berlin, Heidelberg. https://doi.org/10.1007/3-540-45428-4_10
Download citation
DOI: https://doi.org/10.1007/3-540-45428-4_10
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-43818-2
Online ISBN: 978-3-540-45428-1
eBook Packages: Springer Book Archive