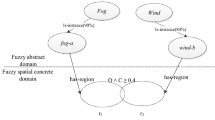
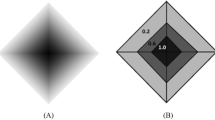
Abstract
For a long time topological predicates between spatial objects have been a main area of research on spatiald ata handling, reasoning, and query languages. But these predicates still suffer from two main restrictions: first, they are only applicable to simplified abstractions of spatial objects like single points, continuous lines, and simple regions, as they occur in systems like current geographical information systems and spatial database systems. Since these abstractions are usually not suficient to cope with the complexity of geographic reality, their generalization is needed which especially has influence on the nature and definition of their topological relationships. This paper gives a formal definition of complex crisp regions, which may consist of several components and which may have holes, and it especially shows how topologicalpre dicates can be defined on them. Second, topological predicates so far only operate on crisp but not on fuzzy spatial objects which occur frequently in geographical reality. Based on complex crisp regions, this paper gives a definition of their fuzzy counterparts and shows how topological predicates can be defined on them.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
D. Altman. Fuzzy Set Theoretic Approaches for Handling Imprecision in Spatial Analysis. Int. Journal of Geographical Information Systems, 8(3):271–289, 1994.
P. A. Burrough and A. U. Frank, editors. Geographic Objects with Indeterminate Boundaries. GISDATA Series, vol. 2. Taylor & Francis, 1996.
E. Clementini, P. Di Felice, and G. Califano. Composite Regions in Topological Queries. Information Systems, 20(7):579–594, 1995.
E. Clementini and P. Di Felice. An Algebraic Model for Spatial Objects with Indeterminate Boundaries, pages 153–169. In Burrough and Frank [2], 1996.
D. Dubois and M.-C. Jaulent. A General Approach to Parameter Evaluation in Fuzzy DigitalPictures. Pattern Recognition Letters, pages 251–259, 1987.
M. J. Egenhofer. A Formal Definition of Binary Topological Relationships. In 3rd Int. Conf. on Foundations of Data Organization and Algorithms, LNCS 367, pages 457–472. Springer-Verlag, 1989.
M.J. Egenhofer, E. Clementini, and P. Di Felice. Topological Relations between Regions with Holes. Int. Journal of Geographical Information Systems, 8(2):128–142, 1994.
M. Erwig and M. Schneider. Vague Regions. In 5th Int. Symp. on Advances in Spatial Databases, LNCS 1262, pages 298–320. Springer-Verlag, 1997.
S. Gaal. Point Set Topology. Academic Press, 1964.
R. H. Güting and M. Schneider. Realms: A Foundation for Spatial Data Types in Database Systems. In 3rd Int. Symp. on Advances in Spatial Databases, LNCS 692, pages 14–35. Springer-Verlag, 1993.
M. Schneider. Modelling Spatial Objects with Undetermined Boundaries Using the Realm/ROSE Approach, pages 141–152. In Burrough and Frank [2], 1996.
M. Schneider. Spatial Data Types for Database Systems — Finite Resolution Geometry for Geographic Information Systems, volume LNCS 1288. Springer-Verlag, Berlin Heidelberg, 1997.
M. Schneider. Uncertainty Management for SpatialDa ta in Databases: Fuzzy SpatialDa ta Types. In 6th Int. Symp. on Advances in Spatial Databases, LNCS 1651, pages 330–351. Springer-Verlag, 1999.
M. Schneider. Finite Resolution Crisp and Fuzzy Spatial Objects. In Int. Symp. on Spatial Data Handling, pages 5a.3–17, 2000.
R. B. Tilove. Set Membership Classifition: A Unified Approach to Geometric Intersection Problems. IEEE Trans. on Computers, C-29:874–883, 1980.
M. Worboys. Imprecision in Finite Resolution Spatial Data. GeoInformatica, 2(3):257–279, 1998.
L. A. Zadeh. Fuzzy Sets. Information and Control, 8:338–353, 1965.
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2001 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Schneider, M. (2001). A Design of Topological Predicates for Complex Crisp and Fuzzy Regions. In: S.Kunii, H., Jajodia, S., Sølvberg, A. (eds) Conceptual Modeling — ER 2001. ER 2001. Lecture Notes in Computer Science, vol 2224. Springer, Berlin, Heidelberg. https://doi.org/10.1007/3-540-45581-7_10
Download citation
DOI: https://doi.org/10.1007/3-540-45581-7_10
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-42866-4
Online ISBN: 978-3-540-45581-3
eBook Packages: Springer Book Archive