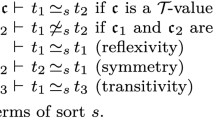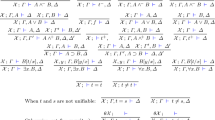Abstract
Decision procedures for combinations of theories are at the core of many modern theorem provers such as ACL2, Ehdm, PVS, SIMPLIFY, the Stanford Pascal Verifier, STeP, SVC, and Z/Eves. Shostak, in 1984, published a decision procedure for the combination of canonizable and solvable theories. Recently, Ruess and Shankar showed Shostak’s method to be incomplete and nonterminating, and presented a correct version of Shostak’s algorithm along with informal proofs of termination, soundness, and completeness. We describe a formalization and mechanical verification of these proofs using the PVS verification system. The formalization itself posed significant challenges and the verification revealed some gaps in the informal argument.
This work was funded by NSF Grant CCR-0082560, DARPA/AFRL Contract F33615-00-C-3043, and NASA Contract NAS1-00079. Sam Owre, Harald Rueß, and John Rushby of SRI provided insightful comments on earlier drafts. We thank the anonymous referees for their constructive criticism.
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
R. S. Boyer and J. S. Moore. A Computational Logic. Academic Press, New York, NY, 1979.
R. S. Boyer and J. S. Moore. Metafunctions: Proving them correct and using them efficiently as new proof procedures. In R. S. Boyer and J. S. Moore, editors, The Correctness Problem in Computer Science. Academic Press, London, 1981.
David Cyrluk, Patrick Lincoln, and N. Shankar. On Shostak’s decision procedure for combinations of theories. In M. A. McRobbie and J. K. Slaney, editors, Automated Deduction—CADE-13, volume 1104 of Lecture Notes in Artificial Intelligence, pages 463–477, New Brunswick, NJ, July/August 1996. Springer-Verlag.
J. Ford and I. A. Mason. Establishing a General Context Lemma in PVS. In Proceedings of the 2nd Australasian Workshop on Computational Logic, AWCL’01, 2001. submitted.
J. Ford and I. A. Mason. Operational techniques in PVS—a preliminary evaluation. In Proceedings of the Australasian Theory Symposium, CATS’ 01, Gold Coast, Queensland, Australia, January-February 2001.
J.-C. Filliâtre, S. Owre, H. Rueß, and N. Shankar. ICS: Integrated Canonization and Solving. In G. Berry, H. Comon, and A. Finkel, editors, Computer-Aided Verification, CAV’ 2001, volume 2102 of Lecture Notes in Computer Science, pages 246–249, Paris, France, July 2001. Springer-Verlag.
M. Gordon, R. Milner, and C. Wadsworth. Edinburgh LCF: A Mechanized Logic of Computation, volume 78 of Lecture Notes in Computer Science. Springer-Verlag, 1979.
G. Nelson and D. C. Oppen. Simplification by cooperating decision procedures. ACM Transactions on Programming Languages and Systems, 1(2):245–257, 1979.
S. Owre, J. M. Rushby, and N. Shankar. PVS: A prototype verification system. In Deepak Kapur, editor, 11th International Conference on Automated Deduction (CADE), volume 607 of Lecture Notes in Artificial Intelligence, pages 748–752, Saratoga, NY, June 1992. Springer-Verlag.
Harald Rueß and Natarajan Shankar. Deconstructing Shostak. In 16th Annual IEEE Symposium on Logic in Computer Science, pages 19–28, Boston, MA, July 2001. IEEE Computer Society.
N. Shankar. Towards mechanical metamathematics. Journal of Automated Reasoning, 1(4):407–434, 1985.
N. Shankar. Efficiently executing PVS. Project report, Computer Science Laboratory, SRI International, Menlo Park, CA, November 1999. Available at http://www.csl.sri.com/shankar/PVSeval.ps.gz.
Robert E. Shostak. Deciding combinations of theories. Journal of the ACM, 31(1):1–12, January 1984.
Laurent Théry. A certified version of Buchberger’s algorithm. In H. Kirchner and C. Kirchner, editors, Proceedings of CADE-15, number 1421 in Lecture Notes in Artificial Intelligence, pages 349–364, Berlin, Germany, July 1998. Springer-Verlag.
K.N. Verma and J. Goubault-Larrecq. Reflecting BDDs in Coq. Technical Report 3859, INRIA, Rocquencourt, France, January 2000.
F. W. von Henke, S. Pfab, H. Pfeifer, and H. Rueß. Case studies in meta-level theorem proving. In Jim Grundy and Malcolm Newey, editors, Proc. Intl. Conf. on Theorem Proving in Higher Order Logics, number 1479 in Lecture Notes in Computer Science, pages 461–478. Springer-Verlag, September 1998.
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2002 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Ford, J., Shankar, N. (2002). Formal Verification of a Combination Decision Procedure. In: Voronkov, A. (eds) Automated Deduction—CADE-18. CADE 2002. Lecture Notes in Computer Science(), vol 2392. Springer, Berlin, Heidelberg. https://doi.org/10.1007/3-540-45620-1_29
Download citation
DOI: https://doi.org/10.1007/3-540-45620-1_29
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-43931-8
Online ISBN: 978-3-540-45620-9
eBook Packages: Springer Book Archive