Abstract
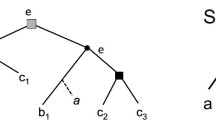
The input to a supertree problem is a collection of phyloge-netic trees that intersect pairwise in their leaf sets; the goal is to construct a single tree that retains as much as possible of the information in the input. This task is complicated by inconsistencies due to errors. We consider the case where the source trees are rooted and are represented by the clusters they exhibit. The problem is to find the minimum number of flips needed to resolve all inconsistencies, where each flip moves a taxon into or out of a cluster. We prove that the minimum flip problem is \( \mathcal{N}\mathcal{P} \) -complete, but show that it is fixed-parameter tractable and give an approximation algorithm for a special case.
Research of D. Chen, O. Eulenstein, and M. Sanderson supported in part by the National Science Foundation (NSF) under grant no. 0075319. D. Fernández-Baca was supported in part by NSF under grant CCR-9520946.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
A. V. Aho, Y. Sagiv, T. G. Szymanski, and J. D. Ullman, Inferring a tree from lowest common ancestors with an application to the optimization of relational expressions, SIAM Journal on Computing 10 (1981), no. 3, 405–421.
B. R. Baum, Combining trees as a way of combining data sets for phylogenetic inference, and the desirability of combining gene trees, Taxon 41 (1992), 3–10.
O. R. P. Bininda-Emonds, J. L. Gittleman, and A. Purvis, Building large trees by combining phylogenetic information: a complete phylogeny of the extant Carnivora (Mammalia), Biol. Rev. 74 (1999), 143–175.
D. R. Brooks, Hennig’s parasitological method: a proposed solution, Syst. Zool. 30 (1981), 325,331.
David Bryant, John Tsang, Paul E. Kearney, and Ming Li, Computing the quartet distance between evolutionary trees, Symposium on Discrete Algorithms, 2000, pp. 285–286.
D. Chen, O. Eulenstein, D.Fernández-Baca, and M. Sanderson, http://genome.cs.iastate.edu/supertree.
—, Supertrees by flipping, Tech. Report TR02-01, Iowa State University, Dept. of Computer Science, Iowa State University, Department of Computer Science, 226 Atanasoff Hall, Ames, IA 50011-1040 USA, January 2002.
M. J. Donoghue, Phylogenies and the analysis of evolutionary sequences, with examples from seed plants, Evolution 43 (1989), 1137–1156.
R. G. Downey and M. R. Fellows, Parameterized compllexity, Springer, 1997.
G. F. Estabrook, C. Johnson, and F. R. McMorris, An idealized concept of the true cladistic character?, Mathematical Bioscience 23 (1975), 263–272.
J. S. Farris, On comparing the shapes of taxonomic trees, Systematic Zoology 22 (1976), 50–54.
J. Felsenstein, PHYLIP homepage, http://evolution.genetics.washington.edu/phylip.html.
A. D. Gordon, Consensus supertrees: the synthesis of rooted trees containing overlapping sets of labelled leaves, J. Classif. 9 (1986), 335–348.
R. L. Graham and L. R. Foulds, Unlikelihood that minimal phylogenies for a realistic biological study can be constructed in reasonable computation time, Math. Biosci. 60 (1982), 133–142.
D. Gusfield, Algorithms on strings, trees, and sequences, Cambridge University Press, 1979.
Henzinger, King, and Warnow, Constructing a tree from homeomorphic subtrees, with applications to computational evolutionary biology, SODA: ACM-SIAM Symposium on Discrete Algorithms (A Conference on Theoretical and Experimental Analysis of Discrete Algorithms), 1996.
M. R. Henzinger, V. King, and T. Warnow, Constructing a tree from homeomorphic subtrees, with applications to computational evolutionary biology, Algorithmica 24 (1999), 1–13.
Sampath Kannan, Tandy Warnow, and Shibu Yooseph, Computing the local consensus of trees, Symposium on Discrete Algorithms, 1995, pp. 68–77.
P. Kearney, M. Li, J. Tsang, and T. Jiang, Recovering branches on the tree of life: An approximation algorithm, SODA, 1999, pp. 537–5465.
F. G. R. Liu, M. M. Miyamoto, N. P. Freire, P. Q. Ong, M. R. Tennant, T. S. Young, and K. F. Gugel, Molecular and morphological supertrees for eutherian (placental) mammals, Science 291 (2001), 1786–1789.
A. Natanzon, R. Shamir, and R. Sharan, Complexity classification of some edge modification problems, Discrete Applied Mathematics 113 (2001), no. 1, 109–128.
A. Ortolani, Spots, stripes, tail tips and dark eyes: predicting the function of carnivore colour patterns using the comparative method, Biol. J. Linn. Soc. 67 (1999), 433–476.
I Pe’er, R. Shamir, and R. Sharan, Incomplete directed perfect phylogeny., Proc. CPM 2000, 2000, pp. 143–153.
A. Purvis, A modification to Baum and Ragan’s method for combining phylogenetic trees, Systematic Biology 44 (1995), 251–255.
M. A. Ragan, Phylogenetic inference based on matrix representation of trees, Molecular Phylogenetics and Evolution 1 (1992), 53–58.
M. J. Sanderson, A. Purvis, and C. Henze, Phylogenetic supertrees: assembling the trees of life, Trends Ecol. Evol. 13 (1998), 105–109.
C. Semple and M. Steel, A supertree method for rooted trees, Discrete Applied Mathematics 105 (2000), 147–158.
M. A. Steel, The complexity of reconstructing trees from qualitative characters and subtrees, Journal of Classification 9 (1992), 91–116.
M. F. Wojciechowski, M. J. Sanderson, K. P. Steele, and A. Liston, Molecular phylogeny of the “temperate herbaceous tribes” of papilionoid legumes: a supertree approach, Adv. Legume Syst., in press.
M. Yannakakis, Computing the minimum fill-in is NP-complete, SIAM Journal on Algebraic and Discrete Methods 2 (1981), no. 1, 77–79.
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2002 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Chen, D., Eulenstein, O., Fernández-Baca, D., Sanderson, M. (2002). Supertrees by Flipping. In: Ibarra, O.H., Zhang, L. (eds) Computing and Combinatorics. COCOON 2002. Lecture Notes in Computer Science, vol 2387. Springer, Berlin, Heidelberg. https://doi.org/10.1007/3-540-45655-4_42
Download citation
DOI: https://doi.org/10.1007/3-540-45655-4_42
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-43996-7
Online ISBN: 978-3-540-45655-1
eBook Packages: Springer Book Archive