Abstract
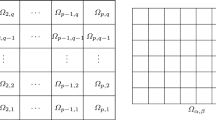
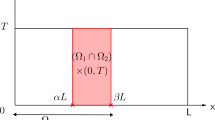
In this paper we study the convergence of the non overlapping domain decomposition for thje solving large linear system arising from semi discretization of two dimentionalinitial valu problem with homogeneous boundary conditions, and solved by implicittime stepping using first and two alternatives of second order FS-methods. The interface values along the artificial boundary condition line are found using explicit forward Eular’s methods for the first order FS metdod,and for the second order FS-method to use extra polation procedure for each spatial variable individually. The solution by the non overlapping domain decomposition with FS-method is applicable to problems that requires the sluotion on non uniform meshes for each spatial variables which will unable us to use different time stepping over different sub domains, and with the possibility of extension to three dimentional problem.
Chapter PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
References
Blum, H., Lisky, S. and Ranacher, R.,” A domain Splitting Algorithm for Parabolic Problems,” Computing, 49:11–23, 1992.
Dawson, C.N., Du, Q., and Dupont, D.F.” A finite Difference Domain Decomposition Algorithm for Numerical Solution of the Heat Equation,” Mathematics of Computation, 57:63–71, 1991.
Gaiffe, S., Glowinski, R. and Lemonnier, P. ” Domain Decomposition and Splitting Methods for Parabolic Problems via a Mixed Formulation”, The 12th International Conference on Domain Cecomposition, Chiba-Japan, 1999.
Gourlay, A. R. and A.R. Mitchell,” The Equivalence of Certain ADI and LOD Difference Methods,” SIAM J. Numer. Anal, 6:37, 1969.
Goudnov, S. K.,” Finite Difference Methods for Numerical Computation of Discontinuous Solutions of the Equations of Fluid Dynamics”, Mat.Sbornik, 47:271–295, 1959.
Hundsdorfer, W.,” Unconditional Convergence of Some Crank-Nicolson LOD Methods for Initial Boundary Value Problems,” Mathematics Of Computation, 58(197):35–53, 1992.
Khan, L.A., and P.L. Liu,” An Operator-Splitting Algorithm for the Three-Dimensional Diffusion Equation,” Numerical methods for Partial Differential Equations 11:617–624, 1995.
Lawson, J. D. and Morris J, LI, ” The Extrapolation of First Order Methods for Parabolic Partial Differential Equations. I,” SIAM J. Numer. Anal. 15:1212–1224, 1978.
Lapidus, L., and Pinder, G.F.: ” Numerical Solution of Partial Differential Equations in Science and Engineering”, John Wiley, 1982.
Meurant, G. A.,” A Domain Decomposition Method for Parabolic Problems,” Applied Numerical Mathematics, 8:427–441, 1991.
Meurant, G. A.,” Numerical Experiments with Domain Decomposition Method for Parabolic Problems on Parallel Computers,” 4 th ”Int. Sypm. on Domain Decomposition methods for Partial Differential Equations,” ed. Glowinski, R., Kunetsov, Y.A., Meurant, G.A., Periaus, J., and Widlund, O.W., SIAM, PA., 394–408, 1991.
Mitchell, A.R. and Griffiths, D.F.,” The Fnite Difference Methods in Partial Differential Equations”, John Wiley, 1980.
Mathew, T.P., Polyakov, P.L., Russo, G., and Wang, J.,” Domain Decomposition Operator Splittings for the Solution of Parabolic Equations,” SIAM J.Sci.Comput. 19:912–932, 1998.
Strang, G.,” Accurate Partial Difference Methods I: Linear Cauchy Problems,” Arch. Rational Mech. Anal, 12:392–402, 1963.
Strang, G.,” On the construction and Comparison of Difference Schemes,” SIAM J. Numer. Anal, 5:506–517, 1968.
Swayne, D.A.,” Time Dependent Boundary and Interior Forcing in Locally One Dimensional Schemes,” SIAM J.Sci.Stat.Comput, 8:755–767, 1987.
Yanenko, N.N.,” The method of Fractional Steps; The Solution of Problems of Mathematical Physics in Several Variables”, Springer Verlag, 1971.
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2002 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Daoud, D.S., Subasi, D.S. (2002). A Fractional Splitting Algorithm for Non-overlapping Domain Decomposition. In: Sloot, P.M.A., Hoekstra, A.G., Tan, C.J.K., Dongarra, J.J. (eds) Computational Science — ICCS 2002. ICCS 2002. Lecture Notes in Computer Science, vol 2329. Springer, Berlin, Heidelberg. https://doi.org/10.1007/3-540-46043-8_32
Download citation
DOI: https://doi.org/10.1007/3-540-46043-8_32
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-43591-4
Online ISBN: 978-3-540-46043-5
eBook Packages: Springer Book Archive