Abstract
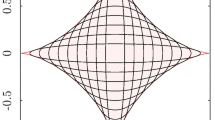
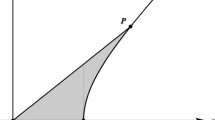
In this paper, a new method for interrogation of parametric surfaces is introduced. The basic idea is to consider the distance measured on certain curves on a surface as an interrogation tool. To this aim, two different sets of characteristic curves are considered: the normal section curves and the geodesic curves. The differential equations of these sets of curves starting radially from a given point of the surface are stated. Then, they are solved numerically, introducing the arc-length on the surface as the integration variable. Associated with those curves we construct the polar isodistance curves which are obtained by joining the points at the same distance from a given point of the surface along the section or geodesic curves. Finally, some illustrative examples for NURBS surfaces, by far the most common surfaces in industry, are also described.
This research was supported by the CICYT of the Spanish Ministry of Education (projects TAP1998-0640 and DPI2001-1288) and the European Fund FEDER (Contract 1FD1997-0409).
Chapter PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
References
Beck, J.M., Farouki, R.T., Hinds, J.K.: Surface analysis methods. IEEE Computer Graphics and Applications, Dec. (1986) 18–36
Farin, G.E.: Curves and Surfaces for Computer-Aided Geometric Design, 5th ed. Morgan Kaufmann, San Francisco (2001)
Grandine, T.A., Klein, F.W.: A new approach to the surface intersection problem. CAGD 14 (1997) 111–134
Hagen, H., Schreiber, T., Gschwind, E.: Methods for surface interrogation. Proc. Visualization’90, IEEE Computer Society Press, Los Alamitos, Calif. (1990) 187–193
Hagen, H., Hahman, S., Schreiber, T., Nakajima, Y., Wördenweber, B., Hollemann-Grundstedt, P.: Surface interrogation algorithms. IEEE Computer Graphics and Applications, Sept. (1992) 53–60
Hoschek, J., Lasser, D.: Computer-Aided Geometric Design, A.K. Peters, Wellesley, MA (1993)
Klass, R.: Correction of local surface irregularities using reflection lines. CAD, 12(2) (1980) 73–77
Koenderink, J.J., van Doorn, A.J.: Surface shapes and curvature scales. Image and Vision Computing, 8(2) (1992) 557–565
Kriezis, G.A., Patrikalakis, N.M., Wolter, F.E.: Topological and differential equation methods for surface intersections. CAD, 24(1) (1992) 41–55
Lee, R.B., Fredricks, D.A.: Intersection of parametric surfaces and a plane. IEEE Computer Graphics and Applications, Aug. (1984) 48–51
The Mathworks Inc: Using Matlab. Natick, MA (1999)
Munchmeyer, F.C., Haw, R.: Applications of differental geometry to ship design. In: Computer Applications in the Automation of Shipyard Operation and Ship Design IV, Rogers, D.F., et al. (eds.) North Holland, Amsterdam (1982) 183–188
Patrikalakis, N.M., Bardis, L.: Offsets of curves on rational B-spline surfaces. Engineering with Computers, 5 (1989) 39–46
Petersen, C.S.: Adaptive contouring of three-dimensional surfaces. CAGD 1(1) (1984) 61–74
Piegl, L., Tiller, W.: The NURBS Book, Springer Verlag, Berlin Heidelberg (1997)
Poeschl, T.: Detecting surface irregularities using isophotes. CAGD 1(2) (1984) 163–168
Satterfield, S.G., Rogers, D.F.: A procedure for generating contour lines from a B-spline surface. IEEE Computer Graphics and Applications, Apr. (1985) 71–75
Struik, D.J.: Lectures on Classical Differential Geometry, 2nd ed., Dover Publications, New York (1988)
Theisel, H., Farin, G.E.: The curvature of characteristic curves on surfaces. IEEE Computer Graphics and Applications, Nov./Dec. (1997) 88–96
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2002 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Puig-Pey, J., Gálvez, A., Iglesias, A. (2002). Polar Isodistance Curves on Parametric Surfaces. In: Sloot, P.M.A., Hoekstra, A.G., Tan, C.J.K., Dongarra, J.J. (eds) Computational Science — ICCS 2002. ICCS 2002. Lecture Notes in Computer Science, vol 2330. Springer, Berlin, Heidelberg. https://doi.org/10.1007/3-540-46080-2_17
Download citation
DOI: https://doi.org/10.1007/3-540-46080-2_17
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-43593-8
Online ISBN: 978-3-540-46080-0
eBook Packages: Springer Book Archive