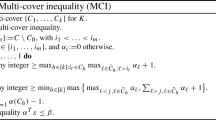Abstract
A cardinality constrained knapsack problem is a continuous knapsack problem in which no more than a specified number of non-negative variables are allowed to be positive. This structure occurs, for example, in areas such as finance, location, and scheduling. Traditionally, cardinality constraints are modeled by introducing auxiliary 0-1 variables and additional constraints that relate the continuous and the 0-1 variables. We use an alternative approach, in which we keep in the model only the continuous variables, and we enforce the cardinality constraint through a specialized branching scheme and the use of strong inequalities valid for the convex hull of the feasible set in the space of the continuous variables. To derive the valid inequalities, we extend the concepts of cover and cover inequality, commonly used in 0-1 programming, to this class of problems, and we show how cover inequalities can be lifted to derive facet-defining inequalities. We present three families of non-trivial facet-defining inequalities that are lifted cover inequalities. Finally, we report computational results that demonstrate the effectiveness of lifted cover inequalities and the superiority of the approach of not introducing auxiliary 0-1 variables over the traditional MIP approach for this class of problems.
This research was partially supported by NSF grants DMI-0100020 and DMI-0121495. An expanded version of this report can be found in [15].
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
E. Balas, “Facets of the Knapsack Polytope,” Mathematical Programming 8, 146–164 (1975).
E. Balas, S. Ceria, G. Cornuéjols, and N. Natraj, “Gomory Cuts Revisited,” Operations Research Letters 19, 1–9 (1996).
E.L.M. Beale, “Integer Programming,” in: K. Schittkowski (Ed.), Computational Mathematical Programming, NATO ASI Series, Vol. F15, Springer-Verlag, 1985, pp. 1–24.
E.L.M. Beale and J.A. Tomlin, “Special Facilities in a General Mathematical Programming System for Nonconvex Problems Using Ordered Sets of Variables,” in: J. Lawrence (Ed.), Proceedings of the fifth Int. Conf. on O.R., Tavistock Publications, 1970, pp. 447–454.
L.T. Biegler, I.E. Grossmann, and A.W. Westerberg, Systematic Methods of Chemical Process Design, Prentice Hall, 1997.
D. Bienstock, “Computational Study of a Family of Mixed-Integer Quadratic Programming Problems,” Mathematical Programming 74, 121–140 (1996).
H. Crowder, E.L. Johnson, and M.W. Padberg, “Solving Large Scale Zero-One Problems,” Operations Research 31, 803–834 (1983).
G.B. Dantzig, “On the significance of Solving Linear Programming Problems with some Integer Variables,” Econometrica 28, 30–44 (1960).
I.R. de Farias, Jr., “A Polyhedral Approach to Combinatorial Complementarity Programming Problems,” Ph.D. Thesis, School of Industrial and Systems Engineering, Georgia Institute of Technology, Atlanta, GA (1995).
I.R. de Farias, Jr., “A Family of Facets for the Uncapacitated p-Median Polytope,” Operations Research Letters 28, 161–167 (2001).
I.R. de Farias, Jr., E.L. Johnson, and G.L. Nemhauser “A Generalized Assignment Problem with Special Ordered Sets: A Polyhedral Approach,” Mathematical Programming 89, 187–203 (2000).
I.R. de Farias, Jr., E.L. Johnson, and G.L. Nemhauser “Branch-and-Cut for Combinatorial Optimization Problems without Auxiliary Binary Variables,” Knowledge Engineering Review 16, 25–39 (2001).
I.R. de Farias, Jr., E.L. Johnson, and G.L. Nemhauser, “Facets of the Complementarity Knapsack Polytope,” to appear in Mathematics of Operations Research.
I.R. de Farias, Jr. and G.L. Nemhauser, “A Family of Inequalities for the Generalized Assignment Polytope,” Operations Research Letters 29, 49–51 (2001).
I.R. de Farias, Jr. and G.L. Nemhauser, “A Polyhedral Study of the Cardinality Constrained Knapsack Problem,” CORE Discussion Paper (2001).
Z. Gu, G.L. Nemhauser, and M.W.P. Savelsbergh, “Lifted Flow Cover Inequalities for Mixed 0-1 Integer Programs,” Mathematical Programming 85, 439–467 (1999).
M. Grötschel, M. Jünger, and G. Reinelt, “A Cutting Plane Algorithm for the Linear Ordering Problem,” Operations Research 32, 1195–1220 (1984).
P.L. Hammer, E.L. Johnson, and U.N. Peled, “Facets of Regular 0-1 Polytopes,” Mathematical Programming 8, 179–206 (1975).
K. Hoffman and M.W. Padberg, “LP-Based Combinatorial Problem Solving,” Annals of Operations Research 4, 145–194 (1985).
J.N. Hooker, G. Ottosson, E.S. Thornsteinsson, and H.-J. Kim, “A Scheme for Unifying Optimization and Constraint Satisfaction Methods,” Knowledge Engineering Review 15, 11–30 (2000).
H. Marchand, A. Martin, R. Weismantel, and L.A. Wolsey, “Cutting Planes in Integer and Mixed-Integer Programming,” CORE Discussion Paper (1999).
H.M. Markowitz and A.S. Manne, “On the Solution of Discrete Programming Problems,” Econometrica 25, 84–110 (1957).
G.L. Nemhauser, G.C. Sigismondi, and M.W.P. Savelsbergh, “MINTO, a Mixed-INTeger Optimizer,” Operations Research Letters 15, 47–58 (1994).
G.L. Nemhauser and L.A. Wolsey, Integer Programming and Combinatorial Optimization, John Wiley and Sons, 1988.
M.W. Padberg, “A Note on Zero-One Programming,” Operations Research 23, 883–837 (1975).
M.W. Padberg and G. Rinaldi, “Optimization of a 532-City Symmetric Traveling Salesman Problem by Branch-and-Cut,” Operations Research Letters 6, 1–7 (1987).
A.F. Perold, “Large-Scale Portfolio Optimization,” Management Science 30, 1143–1160 (1984).
R. Raman and I.E. Grossmann, “Symbolic Integration of Logic in MILP Branch-and-Bound Methods for the Synthesis of Process Networks,” Annals of Operations Research 42, 169–191 (1993).
M.W.P. Savelsbergh, “Functional Description of MINTO, a Mixed INTeger Optimizer (version 3.0),” http://udaloy.isye.gatech.edu/mwps/projects/minto.html.
P. van Hentenryck, Constraint Satisfaction in Logic Programming, MIT Press, 1989.
T.J. van Roy and L.A. Wolsey, “Solving Mixed-Integer Programming Problems Using Automatic Reformulation,” Operations Research 35, 45–57 (1987).
L.A. Wolsey, “Faces for a Linear Inequality in 0-1 Variables,” Mathematical Programming, 8 165–178 (1975).
L.A. Wolsey, “Facets and Strong Valid Inequalities for Integer Programs,” Operations Research 24, 367–372 (1976).
L.A. Wolsey, Integer Programming, John Wiley and Sons, 1998.
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2002 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
de Farias, I.R., Nemhauser, G.L. (2002). A Polyhedral Study of the Cardinality Constrained Knapsack Problem. In: Cook, W.J., Schulz, A.S. (eds) Integer Programming and Combinatorial Optimization. IPCO 2002. Lecture Notes in Computer Science, vol 2337. Springer, Berlin, Heidelberg. https://doi.org/10.1007/3-540-47867-1_21
Download citation
DOI: https://doi.org/10.1007/3-540-47867-1_21
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-43676-8
Online ISBN: 978-3-540-47867-6
eBook Packages: Springer Book Archive