Abstract
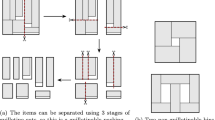
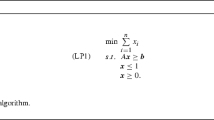
We present an asymptotic PTAS for Two-Dimensional Bin Packing, which requires packing (or cutting) a given set of rectangles from the minimum number of square bins, with the further restriction that cutting the rectangles from the bins can be done in two stages, as is frequently the case in real-world applications. To the best of our knowledge, this is the first approximation scheme for a nontrivial two-dimensional (and real-world) generalization of classical one-dimensional Bin Packing in which rectangles have to be packed in (finite) squares. A simplification of our method yields an asymptotic PTAS for the two-stage packing of rectangles in a bin of unit width and infinite height. Moreover, we point out that our method may lead to a better approximation guarantee for Two-Dimensional Bin Packing without stage restrictions, provided some structural property holds.
This is a preview of subscription content, log in via an institution to check access.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
B.S. Baker, E.G. Coffman, Jr., and R.L. Rivest. Orthogonal packing in two dimensions. SIAM Journal on Computing, 9:846–855, 1980.
B.S. Baker and J.S. Schwartz. Shelf algorithms for two-dimensional packing problems. SIAM Journal on Computing, 12:508–525, 1983.
F.R.K. Chung, M.R. Garey, and D.S. Johnson. On packing two-dimensional bins. SIAM Journal on Algebraic and Discrete Methods, 3:66–76, 1982.
E.G. Coffman, Jr., M.R. Garey, and D.S. Johnson. Approximation algorithms for bin packing: A survey. In D.S. Hochbaum, editor, Approximation Algorithms for NP-Hard Problems. PWS Publishing Company, Boston, 1997.
E.G. Coffman, Jr., M.R. Garey, D.S. Johnson, and R.E. Tarjan. Performance bounds for level-oriented two-dimensional packing algorithms. SIAM Journal on Computing, 9:801–826, 1980.
J.M.V. De Carvalho and A.J.G. Rodrigues. A computer based interactive approach to a two-stage cutting stock problem. INFOR, 32:243–252, 1994.
J.M.V. De Carvalho and A.J.G. Rodrigues. An LP-based approach to a two-stage cutting stock problem. European Journal of Operational Research, 84:580–589, 1995.
W. Fernandez de la Vega and G.S. Lueker. Bin packing can be solved within 1 + ε in linear time. Combinatorica, 1:349–355, 1981.
P.C. Gilmore and R.E. Gomory. Multistage cutting problems of two and more dimensions. Operations Research, 13:94–119, 1965.
N. Karmarkar and R.M. Karp. An efficient approximation scheme for the one-dimensional bin-packing problem. In Proc. 23rd Annual IEEE Symp. Found. Comput. Sci., pages 312–320, 1982.
C. Kenyon and E. Rémila. A near-optimal solution to a two-dimensional cutting stock problem. Mathematics of Operations Research, 25:645–656, 2000.
H.W. Lenstra. Integer programming with a fixed number of variables. Mathematics of Operations Research 8:538–548, 1983.
S.S. Seiden and R. van Stee. New bounds for multi-dimensional packing. In Proc. 13th Annual ACM-SIAM Symp. Discr. Alg. (SODA’02), 485–495, 2002.
F. Vanderbeck. A nested decomposition approach to a 3-stage 2-dimensional cutting stock problem. Management Science, 47:864–879, 2001.
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2002 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Caprara, A., Lodi, A., Monaci, M. (2002). An Approximation Scheme for the Two-Stage, Two-Dimensional Bin Packing Problem. In: Cook, W.J., Schulz, A.S. (eds) Integer Programming and Combinatorial Optimization. IPCO 2002. Lecture Notes in Computer Science, vol 2337. Springer, Berlin, Heidelberg. https://doi.org/10.1007/3-540-47867-1_23
Download citation
DOI: https://doi.org/10.1007/3-540-47867-1_23
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-43676-8
Online ISBN: 978-3-540-47867-6
eBook Packages: Springer Book Archive