Abstract
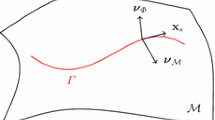
A method for deforming curves in a given image to a desired position in a second image is introduced in this paper. The algorithm is based on deforming the first image toward the second one via a partial differential equation, while tracking the deformation of the curves of in- terest in the first image with an additional, coupled, partial differential equation. The tracking is performed by projecting the velocities of the first equation into the second one. In contrast with previous PDE based approaches, both the images and the curves on the frames/slices of inter- est are used for tracking. The technique can be applied to object tracking and sequential segmentation. The topology of the deforming curve can change, without any special topology handling procedures added to the scheme. This permits for example the automatic tracking of scenes where, due to occlusions, the topology of the objects of interest changes from frame to frame. In addition, this work introduces the concept of project- ing velocities to obtain systems of coupled partial differential equations for image analysis applications. We show examples for object tracking and segmentation of electronic microscopy. We also briefly discuss pos- sible uses of this framework îîfor three dimensional morphing.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
L. Alvarez, P. L. Lions, and J. M. Morel, “Image selective smoothing and edge detection by nonlinear diffusion,” SIAM J. Numer. Anal. 29, pp. 845–866, 1992.
M. Black, G. Sapiro, D. Marimont, and D. Heeger, “Robust anisotropic diffusion,” IEEE Trans. Image Processing 7:3, pp. 421–432, 1998.
A. Blake and M. Isard, Active Contours, Springer-Verlag, New York, 1998.
I. Carlbom, D. Terzopoulos, and K. Harris, “Computer-assisted registration, segmentation, and 3D reconstruction from images of neuronal tissue sections,” IEEE Transactions on Medical Imaging 13:2, pp. 351–362, 1994.
V. Caselles, R. Kimmel, and G. Sapiro, “Geodesic active contours,” International Journal of Computer Vision 22:1, pp. 61–79, 1997.
Y. G. Chen, Y. Giga, and S. Goto, “Uniqueness and existence of viscosity solutions of generalized mean curvature flow equations,” J. Di_. Geom. 33, 1991.
L. C. Evans and J. Spruck, “Motion of level sets by mean curvature, I,” J. Diff. Geom. 33, 1991.
M. Kass, A. Witkin, and D. Terzopoulos, “Snakes: Active contour models,” International Journal of Computer Vision 1, pp. 321–331, 1988.
S. Kichenassamy, A. Kumar, P. Olver, A. Tannenbaum, and A. Yezzi, “Conformal curvature flows: from phase transitions to active vision,” Archive for Rational Mechanics and Analysis 134, pp. 275–301, 1996.
R. Malladi, J. A. Sethian and B. C. Vemuri, “Shape modeling with front propagation: A level set approach,” IEEE-PAMI 17, pp. 158–175, 1995.
S. J. Osher and J. A. Sethian, “Fronts propagation with curvature dependent speed: Algorithms based on Hamilton-Jacobi formulations,” Journal of Computational Physics 79, pp. 12–49, 1988.
N. Paragios and R. Deriche, “A PDE-based level-set approach for detection and tracking of moving objects,” Proc. Int. Conf. Comp. Vision’ 98, Bombay, India, January 1998.
N. Paragios and R. Deriche, “Geodesic active regions for motion estimation and tracking,” Technical Report-INRIA-Sophia Antipolis 3631, March 1999.
P. Perona and J. Malik, “Scale-space and edge detection using anisotropic diffusion,” IEEE-PAMI 12, pp. 629–639, 1990.
B. Romeny, Editor, Geometry Driven Diffusion in Computer Vision, Kluwer, The Netherlands, 1994.
M. Proesmans, E. Pauwels, and L. van Gool, “Coupled geometry-driven diffusion equations for low-level vision,” in [15].
L. Vazquez, G. Sapiro, and G. Randall, “Segmenting neurons in electronic microscopy via geometric tracing,” Proc. IEEE ICIP, Chicago, October 1998.
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 1999 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Bertalmio, M., Sapiro, G., Randall, G. (1999). Morphing Active Contours. In: Nielsen, M., Johansen, P., Olsen, O.F., Weickert, J. (eds) Scale-Space Theories in Computer Vision. Scale-Space 1999. Lecture Notes in Computer Science, vol 1682. Springer, Berlin, Heidelberg. https://doi.org/10.1007/3-540-48236-9_5
Download citation
DOI: https://doi.org/10.1007/3-540-48236-9_5
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-66498-7
Online ISBN: 978-3-540-48236-9
eBook Packages: Springer Book Archive