Skip to main content
SpringerLink
Log in

Design of Totally Self-Checking Code-Disjoint Synchronous Sequential Circuits

  • Conference paper
  • First Online:
Dependable Computing — EDCC-3 (EDCC 1999)

Part of the book series: Lecture Notes in Computer Science ((LNCS,volume 1667))

Included in the following conference series:

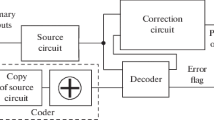
Abstract

Several design methods of self-checking synchronous sequential circuits (SMs) have been proposed in the literature. In this paper, we present a new approach to designing totally self-checking (TSC) code-disjoint (CD) SMs protected against errors using unordered codes. It is assumed that D flip-flops are used as the memory elements and that the circuit should be TSC for all single stuck-at faults (except for the faults on the clock lines), and CD for all input unidirectional errors. The initial 2-level AND-OR equations (with all products shared) are checked for self-testing by verifying some algebraic conditions. All stuck-at-1 faults which cannot be detected during normal functioning are identified. Then, the circuit is modified to the AND-AND-OR circuit with generally higher fault coverage. The resulting circuit is minimized using the well known SIS CAD tools. The whole design process has been automated by using the newely developed software tools that accept the BLIF representation of a SM and are compatible with the SIS tools. Many benchmark SMs can now be implemented as TSC with 100% fault coverage.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution
Chapter
USD 29.95
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever
eBook
USD 39.99
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever
Softcover Book
USD 54.99
Price excludes VAT (USA)
  • Compact, lightweight edition
  • Dispatched in 3 to 5 business days
  • Free shipping worldwide - see info

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Preview

Unable to display preview. Download preview PDF.

Unable to display preview. Download preview PDF.

References

  1. E. S. Sogomonyan and E. V. Slabakov, Self-Checking Devices and Fault-Tolerant Systems, Radio i Svyaz, Moscow, 1989 (in Russian).

    Google Scholar 

  2. M. Diaz, “Design of totally self-checking and fail-safe sequential machines,” in Dig. Pap. 4th Int. FTC Symp., Urbana, IL, 1974, pp. 3-19–3-24.

    Google Scholar 

  3. M. Diaz et al., “Unified design of self-checking and fail-safe combinational circuits and sequential machines,” IEEE Trans. Comput., vol. C-28, pp. 276–281, March 1979.

    Article  Google Scholar 

  4. F. Özgüner, “Design of totally self-checking asynchronous and synchronous sequential machines,” in Dig. Pap. 7th Int. FTC Symp., June 1977, pp. 124–129.

    Google Scholar 

  5. V. I. Maznev, “Synthesis of totally self-checking sequential circuits,” Autom. Remote Control, vol. 38, pp. 913–920, No. 6, 1977.

    MathSciNet  Google Scholar 

  6. V. V. Sapozhnikov, Vl. V. Sapozhnikov, and V. G. Trokhov, “Design of self-checking sequential networks,” Avtom. Vychisl. Tekh., vol. 11, pp. 6–11, No. 3, 1977.

    Google Scholar 

  7. R. David and P. Thevenod-Fosse, “Design of totally self-checking asynchronous modular circuits,” J. Des. Autom. Fault-Tolerant Comput., vol. 4, pp. 271–287, Oct. 1978.

    Google Scholar 

  8. V. V. Sapozhnikov and Vl. V. Sapozhnikov, “Synthesis of totally self-checking asynchronous automata,” Autom. Remote Control, vol. 40, pp. 124–133, No. 1, 1979.

    MATH  MathSciNet  Google Scholar 

  9. V. V. Sapozhnikov and Vl. V. Sapozhnikov, Discrete Automata with Error Detection, Energoatomizdat, Leningrad, SU, 1984 (in Russian).

    Google Scholar 

  10. T. Nanya and T. Kawamura, “A note on strongly fault secure sequential circuits,” IEEE Trans. Comput., vol. C-36, pp. 1121–1123, Sept. 1987.

    Google Scholar 

  11. N. K. Jha and S.-J. Wang, “Design and synthesis of self-checking VLSI circuits,” IEEE Trans. Comp.-Aided Des., vol. 12, pp. 878887, June 1993.

    Google Scholar 

  12. C.-S. Lai and C.-L. Wey, “SOLiT: an automated system for synthesising reliable sequential circuits with multilevel logic implementation,” IEE Proc.-Comput. Digit. Tech., vol. 142, pp. 4954, Jan. 1995.

    Google Scholar 

  13. V. V. Danilov et al., “An algebraic model for the hardware monitoring of automata,” Autom. Remote Control, vol. 36, pp. 984–981, No. 6, 1975.

    MATH  MathSciNet  Google Scholar 

  14. J. Viaud and R. David, “Sequentially self-checking circuits,” in Dig. Pap. 10th Int. FTC Symp., Kyoto, Japan, Oct. 1980, pp. 263–268.

    Google Scholar 

  15. N. S. Shcherbakov and B. P. Podkopaev, Structural Theory of Hardware Checking of Digital Devices, Mashinostroenie, Moscow, 1982 (in Russian).

    Google Scholar 

  16. R. A. Parekhji, G. Venkatesh, and S. D. Sherlekar, “Concurrent error detection using monitoring machines,” IEEE Design and Test of Computers, vol. 12, No. 3, pp. 24–32, Fall 1995.

    Article  Google Scholar 

  17. J. M. Berger, “A note on error detection codes for asymmetric binary channels,” Inform. Contr., vol. 4, pp. 68–73, Mar. 1961.

    Article  MATH  Google Scholar 

  18. C. V. Freiman, “Optimal error detection codes for completely asymmetric binary channels,” Inform. Contr., vol. 5, pp. 64–71, Mar. 1962.

    Article  MATH  MathSciNet  Google Scholar 

  19. J. E. Smith, “The design of totally self-checking check circuits for a class of un-ordered codes,” J. Des. Autom. Fault-Tolerant Comput., vol. 2, pp. 321–342, Oct. 1977.

    Google Scholar 

  20. G. P. Mak, J. A. Abraham, and E. S. Davidson, “The design of PLAs with concurrent error detection,” in Dig. Pap. 12th Int. FTC Symp., Santa Monica, CA, June 1982, pp. 303–310.

    Google Scholar 

  21. J. E. Smith, “On separable unordered codes,” IEEE Trans. Comput., vol. C-33, pp. 741–743, Aug. 1984.

    Google Scholar 

  22. S. J. Piestrak, “Design of TSC code-disjoint inverter-free PLA’s for separable un-ordered codes,” in Proc. ICCD’94, Int. Conf. on Computer Design: VLSI in Com-puters & Processors, Cambridge, MA, Oct. 10-12, 1994, pp. 128–131.

    Google Scholar 

  23. W. C. Carter and P. R. Schneider, “Design of dynamically checked computers,” in Proc. IFIP Conf., Edinburgh, Scotland, Aug. 1968, pp. 878–883.

    Google Scholar 

  24. S. J. Piestrak, Design of Self-Testing Checkers for Unidirectional Error Detecting Codes, Scientific Papers of Inst. of Techn. Cybern. of Techn. Univ. of Wroc law, No. 92, Ser.: Monographs No. 24, Oficyna Wyd. Polit. Wroc l., Wroc law 1995, 112 pp.

    Google Scholar 

  25. S. J. Piestrak, “Design of encoders and self-testing checkers for some systematic unidirectional error detecting codes,” J. of Microelectronic Systems Integration, Sp. Issue on Defect and Fault Tolerance in VLSI Systems, vol. 5, pp. 247–260, No. 4, 1997.

    Google Scholar 

  26. J. F. Wakerly, Error Detecting Codes, Self-Checking Circuits and Applications, North-Holland, New York, 1978.

    Google Scholar 

  27. M. A. Marouf and A. D. Friedman, “Design of self-checking checkers for Berger codes,” in Dig. Pap. 8th Int. FTC Symp., Toulouse, France, June 1978, pp. 179–184.

    Google Scholar 

  28. J. Khakbaz and E. J. McCluskey, “Self-testing embedded parity checkers,” IEEE Trans. Comput., vol. C-33, pp. 753–756, Aug. 1984.

    Article  Google Scholar 

  29. F. Özgüner, “Design of totally self-checking embedded two-rail code checkers,” Electr. Lett., vol. 27, pp. 382–384, 14th Feb. 1991.

    Article  Google Scholar 

  30. S. J. Piestrak, “Design method of combinational self-testing checkers for a class of incomplete 2-rail codes,” submitted to IEEE Trans. Comput.

    Google Scholar 

  31. V. Rabara, “Design of self-checking checker for 1-out-of-n code (n > 3), ” in Proc. 4th Int. Conf. on Fault-Tolerant Syst. Diagnostics, Brno, Czechoslovakia, Sept. 28-30, 1981, pp. 234240; also appears as: V. V. Sapozhnikov and V. Rabara, “Universal synthesis algorithm for 1=n testers, ” Probl. Inf. Transm., vol. 18, pp. 209218, No. 3, 1982.

    MathSciNet  Google Scholar 

  32. D. A. Anderson and G. Metze, “Design of totally self-checking check circuits for m-out-of-n codes,” IEEE Trans. Comput., vol. C-22, pp. 263–269, Mar. 1973.

    Article  Google Scholar 

  33. S. J. Piestrak, “Design method of self-testing checkers for 1-out-of-n codes, ” in Proc. 6th Int. Conf. on Fault-Tolerant Syst. Diagnostics, Brno, Czechoslovakia, Sept. 1983, pp. 57–63.

    Google Scholar 

  34. S. J. Piestrak, “Design method of totally self-checking checkers for m-out-of-n codes, ” in Dig. Pap. 13th Int. FTC Symp., June 28-30, 1983, Milan, Italy, pp. 162–168.

    Google Scholar 

  35. S. J. Piestrak, “The minimal test set for sorting networks and the use of sorting networks in self-testing checkers for unordered codes,” in Dig. Pap. 20th Int. FTC Symp., Newcastle upon Tyne, UK, June 1990, pp. 457–464.

    Google Scholar 

  36. S. J. Piestrak, “General design procedure of self-testing checkers for all m-out-of-n codes with m ≥ 3 using parallel counters,” in Proc. 4th IEEE Int. On-Line Testing Workshop, July 7-9, 1998, Capri, Italy, pp. 182–186.

    Google Scholar 

  37. S. J. Piestrak, “PLA implementation of totally self-checking circuits using m-out-of-n codes,” in Proc. ICCD’85, Port Chester, N.Y., Oct. 1-3, 1985, pp. 777–781.

    Google Scholar 

  38. S. J. Piestrak, “Design of high-speed and cost-effective self-testing checkers for low-cost arithmetic codes,” IEEE Trans. Comput., vol. C-39, pp. 360–374, March 1990.

    Article  Google Scholar 

  39. S. J. Piestrak, “General design principles of self-testing code-disjoint PLA’s,” Proc. ATS’93 — 2nd Asian Test Symp., Beijing, China, Nov. 18-19, 1993, pp. 287–292.

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Wroclaw University of Technology Institute of Engineering Cybernetics, 50-370, Wroclaw, Poland

    Jerzy W. Greblicki & Stanisław J. Piestrak

Authors
  1. Jerzy W. Greblicki
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Stanisław J. Piestrak
    View author publications

    You can also search for this author in PubMed Google Scholar

Editor information

Editors and Affiliations

  1. Department of Computer Science and Engineering, Czech Technical University in Prague, Karlovo nam 13, CZ-12135, Prague 2, Czech Republic

    Jan Hlavička

  2. Institut für Technische Informatik, Medizinische Universität zu Lübeck, Ratzeburger Allee 160, 23538, Lübeck, Germany

    Erik Maehle

  3. Department of Measurement and Information Systems, Technical University of Budapest, Pázmány P. sétány 1/d, H-1521, Budapest, Hungary

    András Pataricza

Rights and permissions

Reprints and permissions

Copyright information

© 1999 Springer-Verlag Berlin Heidelberg

About this paper

Cite this paper

Greblicki, J.W., Piestrak, S.J. (1999). Design of Totally Self-Checking Code-Disjoint Synchronous Sequential Circuits. In: Hlavička, J., Maehle, E., Pataricza, A. (eds) Dependable Computing — EDCC-3. EDCC 1999. Lecture Notes in Computer Science, vol 1667. Springer, Berlin, Heidelberg. https://doi.org/10.1007/3-540-48254-7_18

Download citation

  • DOI: https://doi.org/10.1007/3-540-48254-7_18

  • Published:

  • Publisher Name: Springer, Berlin, Heidelberg

  • Print ISBN: 978-3-540-66483-3

  • Online ISBN: 978-3-540-48254-3

  • eBook Packages: Springer Book Archive

Publish with us

Policies and ethics

Search

Navigation