Abstract voronoi diagrams and their applications

Abstract

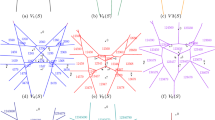
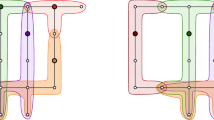
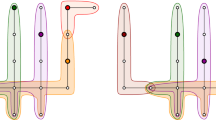
Given a set S of n points in the plane, and for every two of them a separating Jordan curve, the abstract Voronoi diagram V(S) can be defined, provided that the regions obtained as the intersections of all the “halfplanes” containing a fixed point of S are path-connected sets and together form an exhaustive partition of the plane. This definition does not involve any notion of distance. The underlying planar graph, $\hat V$(S), turns out to have O(n) edges and vertices. If S=L ∪ R is such that the set of edges separating L-faces from R-faces in $\hat V$(S) does not contain loops then $\hat V$(L) and $\hat V$(R) can be merged within O(n) steps giving $\hat V$(S). This result implies that for a large class of metrics d in the plane the d-Voronoi diagram of n points can be computed within optimal O(n log n) time. Among these metrics are, for example, the symmetric convex distance functions as well as the metric defined by the city layout of Moscow or Karlsruhe.