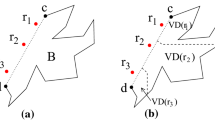
Abstract
Let S be a set of n (possibly intersecting) line segments in the plane. We show that the arrangement of S can be stored implicitly into a data structure of size O(n log2 n) so that the following query can be answered in time O(n 1/2 log2 n): Given two query points, determine whether they lie in the same face of the arrangement of S and, if so, return a path between them that lies within the face. This version of the implicit point location problem is motivated by the following motion planning problem: Given a polygonal robot R with m vertices and a planar region bounded by polygonal obstacles with n vertices in total, preprocess them into a data structure so that, given initial and final positions of R, one can quickly determine whether there exists a continuous collision-free translationsal motion of R from the initial to the final position. We show that such a query can be answered in time O((mn)1/2 log2 mn) using O(mn log2 mn) storage.
Part of this work was done while the second author was visiting the first author at Duke University on a grant of the Netherlands Organization for Scientific Research (N.W.O.). The research of the first author was supported by National Science Foundation Grant CCR-91-06514. The research of the second author was supported by the ESPRIT Basic Research Action No. 3075 (project ALCOM).
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
Agarwal, P. K., Ray shooting and other applications of spanning trees with low stabbing number, SIAM J. Comput. 21 (1992), pp. 540–570.
Agarwal, P. K., Partitioning arrangements of lines II: Applications, Discr. & Comp. Geometry 5 (1990), pp. 533–573.
Aronov, B., H. Edelsbrunner, L. Guibas and M. Sharir, Improved bounds on the complexity of many faces in arrangements of segments, Combinatorial, to appear.
de Berg, M., H. Everett, and H. Wagener, Translation queries for sets of polygons, Tech. Rept. RUU-CS-91-30, Dept. of Comp. Science, Utrecht University, the Netherlands, 1991.
Chazelle, B., H. Edelsbrunner, L. Guibas, M. Sharir, A singly-exponential stratification scheme for real semi-algebraic varieties and its applications, Proc. 16th Int. Coll. Aut. Lang. Prog., Lect. Notes in Comp. Science 372 (1989), pp. 179–193.
Chazelle, B., and J. Friedman, Point location among hyperplanes, manuscript, 1991.
Cheng, S., and R. Janardan, Space-efficient ray-shooting and intersection searching: Algorithms, dynamization, and applications, Proc. 2nd ACM-SIAM Symp. on Discrete Algorithms, (1991), pp. 7–16.
Edelsbrunner, H., L. J. Guibas, J. Hershberger, R. Seidel, M. Sharir, J. Snoeyink, and E. Welzl, Implicitly representing arrangements of lines or segments, Discr. & Comp. Geometry 4 (1989), pp. 433–466.
Edelsbrunner, H., L. J. Guibas, and J. Stolfi, Optimal point location in a monotone subdivision, SIAM J. Comput. 15 (1986), pp. 317–340.
Guibas, L., M. Overmars, and M. Sharir, Ray shooting, implicit point location, and related queries in arrangements of segments, Tech. Rept. 433, New York University, New York, 1989.
Guibas, L., M. Sharir, and S. Sifrony, On the general motion planning problem with two degrees of freedom, Discr. & Comp. Geometry 4 (1989), pp. 491–522.
Hershberger, J. and J. Snoeyink, Computing minimum length paths of a given homotopy class, Proc. 2nd Workshop on Algo. Data Struct. (1991), pp. 331–342.
Kao, T., and D. Mount, An algorithm for computing compacted Voronoi diagrams defined by convex distance functions, Proc. 3rd Canadian Conf. on Comp. Geometry (1991), pp. 104–109.
Leven, D., and M. Sharir, Planning a purely translational motion of a convex object in two-dimensional space using generalized Voronoi diagrams, Discr. & Comp. Geometry 2 (1987), pp. 9–31.
Lozano-Pérez, T., and M. Wesley, An algorithm for planning collision-free paths among polyhedral obstacles, Comm. ACM 22 (1979), pp. 560–570.
Matoušek, J., More on cutting arrangements and spanning trees with low stabbing number, Tech. Rept. B-90-2, Fachbereich Mathematik, Freie Universitaät, Berlin, 1990.
Matoušek, J., Approximations and optimal geometric divide-and-conquer, Proc. 23rd Ann. ACM Symp. Theory of Computing (1991), pp. 506–511.
Matoušek, J., Efficient partition trees, Proc. 7th Ann. ACM Symp. on Comp. Geometry (1991), pp. 1–9.
Mulmuley, K., Randomized multidimensional search trees: Further results in dynamic sampling, Proc. 32nd Ann. IEEE Symp. on Foundations of Computer Science (1991), pp. 216–227.
Preparata, F. P., and M. I. Shamos, Computational Geometry — An Introduction, Springer-Verlag, New York, 1985.
Preparata, F., R. Tamassia, Efficient point location in a convex spatial cell complex, SIAM J. Comput. 21 (1992), pp. 267–280.
Sarnak, N., and R. E. Tarjan, Planar point location using persistent search trees, Comm. ACM 29 (1986), pp. 669–679.
Sifrony, S., A real nearly linear algorithm for translating a convex polygon, Tech. Rept. 476, Dept. Computer Science, New York University, 1989.
Author information
Authors and Affiliations
Editor information
Rights and permissions
Copyright information
© 1992 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Agarwal, P.K., van Kreveld, M. (1992). Implicit point location in arrangements of line segments, with an application to motion planning. In: Shyamasundar, R. (eds) Foundations of Software Technology and Theoretical Computer Science. FSTTCS 1992. Lecture Notes in Computer Science, vol 652. Springer, Berlin, Heidelberg. https://doi.org/10.1007/3-540-56287-7_96
Download citation
DOI: https://doi.org/10.1007/3-540-56287-7_96
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-56287-0
Online ISBN: 978-3-540-47507-1
eBook Packages: Springer Book Archive