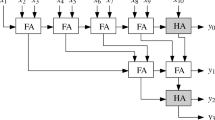
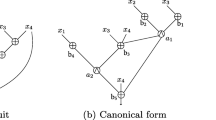
Abstract
Fagin et al. characterized those symmetric Boolean functions which can be computed by small AND/OR circuits of constant depth and unbounded fan-in. Here we provide a similar characterization for d-perceptrons — AND/OR circuits of constant depth and unbounded fan-in with a single MAJORITY gate at the output. We show that a symmetric function has small (quasipolynomial, or \(2^{\log ^{O(1)n} }\) size) d-perceptrons iff it has only poly-log many sign changes (i.e., it changes value logO(1) n times as the number of positive inputs varies from zero to n). A consequence of the lower bound is that a recent construction of Beigel is optimal. He showed how to convert a constant-depth unbounded fan-in AND/OR circuit with poly-log many MAJORITY gates into an equivalent d-perceptron — we show that more than poly-log MAJORITY gates cannot in general be converted to one.
The first author was supported by grants CCR-8812567 and CCR-9008416. The second author was supported by NSF Computer and Computation Theory grants CCR-8922098 and CCR-9207829. The third author was supported in part by the ESPRIT II BRA Programme of the EC under contract 7141 (ALCOM II).
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
M. Ajtai. Σ 11 -formulae on finite structures. Annals of Pure and Applied Logic, 24 (1983), 1–48.
J. Aspnes, R. Beigel, M. Furst and S. Rudich. On the expressive power of voting polynomials. Proceedings of the 23rd Annual Symposium on Theory of Computing (1991), 402–409.
D. A. M. Barrington. Quasipolynomial size circuit classes. Proceedings: Structure in Complexity Theory, Seventh Annual Conference (1992), 86–93.
R. Beigel. Do extra threshold gates help? Proceedings of the 24th Annual Symposium on Theory of Computing (1992), 450–454.
M. Blum and R. Impagliazzo. Generic oracles and oracle classes. Proceedings of the 28th Annual Symposium on Foundations of Computer Science (1987), 118–126.
R. Boppana and M. Sipser. The complexity of finite functions. Handbook of Theoretical Computer Science, Vol. A, ed. by J. van Leeuwen (Elsevier and MIT Press, 1990).
J. Bruck. Harmonic analysis of polynomial threshold functions. SIAM J. Disc. Math. 3:2 (1990), 168–177.
R. Beigel, N. Reingold and D. Spielman. The perceptron strikes back. Proceedings of the 6th Annual Conference on Structrur in Complexity Theory (1991), 286–291.
D. A. Mix Barrington and H. Straubing. Complex polynomials and circuit lower bounds for modular counting. Proceedings of LATIN '92 (1st Latin American Symposium on Theoretical Informatics) (1992), 24–31.
R. Fagin, M. M. Klawe, N. J. Pippenger, and L. Stockmeyer. Bounded depth, polynomial size circuits for symmetric functions. Theoretical Computer Science 36 (1985), 239–250.
M. Furst, J. Saxe, and M. Sipser. Parity, circuits, and the polynomial time hierarchy. Math. System Theory 17 (1984), 13–27.
F. Green. An oracle separating ⊕P from PP PH, Proc. 5th Structure in Complexity Theory (1990), 295–298.
J. Håstad. Computational Limitations of Small-Depth Circuits. (Cambridge, MA, MIT Press, 1986).
J. Hartmanis and L. A. Hemachandra. One-way functions, robustness and non-isomorphism of NP-complete sets. Technical Report DCS TR86-796 (1987), Cornell University.
J. Kahn, G. Kalai, and N. Linial. The influence of variables on boolean functions. Proceedings of 29th Annual ACM Symposium on Theory of Computing (1988), 68–80.
N. Linial, Y. Mansour and N. Nisan. Constant depth circuit, fourier transform and learnability. Proceedings of the 30th Annual IEEE Symposium on Foundations of Computer Science (1989), 574–579.
M. L. Minsky and S. Papert. Perceptrons (Cambridge, MA, MIT Press, 1988). Original edition 1968.
A. A. Razborov. Lower bounds for the the size of circuits of bounded depth with basis ∧, ⊕. Math. Zametki 41:4 (1987), 598–607 (in Russian). English translation Math. Notes Acad. Sci. USSR 41:4 (1987), 333–338.
R. Smolensky. Algebraic methods in the theory of lower bounds for boolean circuit complexity. Proceedings of 19th Annual ACM Symposium on Theory of Computing (1987), 77–82.
G. Tardos. Query complexity, or why is it difficult to separate NP A ∩ co-NP A from P A by a random oracle A? Manuscript (1988).
A. C.-C. Yao. Separating the polynomial-time hierarchy by oracles. Proceedings 26th Annual IEEE Symposium on Foundations of Computer Science (1985), 1–10.
Z.-L. Zhang and D. A. Mix Barrington. Lower bounds for symmetric functions in perceptron-like models. COINS Technical Report 91–81 (1991), University of Massachusetts at Amherst.
Author information
Authors and Affiliations
Editor information
Rights and permissions
Copyright information
© 1993 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Zhang, ZL., Barrington, D.A.M., Tarui, J. (1993). Computing symmetric functions with AND/OR circuits and a single MAJORITY gate. In: Enjalbert, P., Finkel, A., Wagner, K.W. (eds) STACS 93. STACS 1993. Lecture Notes in Computer Science, vol 665. Springer, Berlin, Heidelberg. https://doi.org/10.1007/3-540-56503-5_53
Download citation
DOI: https://doi.org/10.1007/3-540-56503-5_53
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-56503-1
Online ISBN: 978-3-540-47574-3
eBook Packages: Springer Book Archive