Abstract
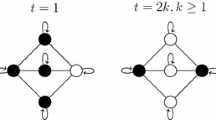
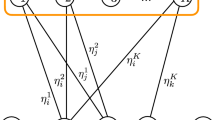
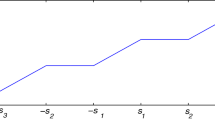
We develop in the present paper a design procedure for neural networks with sparse coefficient matrices. Our results guarantee that the synthesized neural networks have predetermined sparse interconnection structures and store any set of desired memory patterns as reachable memory vectors. We show that a sufficient condition for the existence of a sparse neural network design is self feedback for every neuron in the network. Our design procedure for neural networks with sparse interconnecting structure can take into account various problems encountered in VLSI realizations of such networks. For example, our procedure can be used to design neural networks with few or without any line-crossings resulting from the network interconnections. Several specific examples are included to demonstrate the applicability of the methodology advanced herein.
This work was supported by the National Science Foundation under grant ECS 91-07728.
This is a preview of subscription content, log in via an institution to check access.
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
L. O. Chua, L. Yang, “Cellular Neural Networks: Theory,” IEEE Transactions on Circuits and Systems, Vol. 35, pp. 1257–1272, Oct. 1988
S. R. Das, “On the Synthesis of Nonlinear Continuous Neural Networks,” IEEE Transactions on Systems, Man, and Cybernetics, Vol. 21, pp. 413–418, March/Apr. 1991
J. A. Farrell, A. N. Michel, “A Synthesis Procedure for Hopfield's Continuous-Time Associative Memory,” IEEE Transactions on Circuits and Systems, Vol. 37, pp. 877–884, July 1990
J. J. Hopfield, “Neurons with graded response have collective computational properties like those of two-state neurons,” Proc. Nat. Acad. Sci. USA, Vol. 81, pp. 3088–3092, May 1984
J.-H. Li, A. N. Michel. W. Porod, “Analysis and Synthesis of a Class of Neural Networks: Variable Structure Systems with Infinite Gain,” IEEE Transactions on Circuits and Systems, Vol. 36, pp. 713–731, May 1989
J.-H. Li, A. N. Michel, W. Porod, “Analysis and Synthesis of a Class of Neural Networks: Linear Systems Operating on a Closed Hypercube,” IEEE Transactions on Circuits and Systems, Vol. 36, pp. 1405–1422, Nov. 1989
Derong Liu, A. N. Michel, “Sparsely Interconnected Neural Networks for Associative Memories with Applications to Cellular Neural Networks,” Submitted to IEEE Transactions on Circuits and Systems
A. N. Michel, J. A. Farrell, “Associative Memories via Artificial Neural Networks,” IEEE Control Systems Magazine, Vol. 10, pp. 6–17, Apr. 1990
A. N. Michel, J. Si, G. Yen, “Analysis and Synthesis of a Class of Discrete-Time Neural Networks Described on Hypercubes,” IEEE Transactions on Neural Networks, Vol. 2, pp. 32–46, Jan. 1991
L. Personnaz, I. Guyon, G. Dreyfus, “Collective Computational Properties of Neural Networks: New Learning Mechanisms,” Physical Review A, Vol. 34, pp. 4217–4228, Nov. 1986
F. M. A. Salam, Y. Wang, M.-R. Choi, “On the Analysis of Dynamic Feedback Neural Nets,” IEEE Transactions on Circuits and Systems, Vol. 38, pp. 196–201, Feb. 1991
G. Yen, A. N. Michel, “A Learing and Forgetting Algorithm in Associative Memories: The Eigenstructure Method,” IEEE Transactions on Circuits and Systems-II: Analog and Digital Signal Processing, Vol. 39, pp. 212–225, Apr. 1992
Author information
Authors and Affiliations
Editor information
Rights and permissions
Copyright information
© 1993 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Liu, D., Michel, A.N. (1993). Sparsely interconnected artificial neural networks for associative memories. In: Mira, J., Cabestany, J., Prieto, A. (eds) New Trends in Neural Computation. IWANN 1993. Lecture Notes in Computer Science, vol 686. Springer, Berlin, Heidelberg. https://doi.org/10.1007/3-540-56798-4_140
Download citation
DOI: https://doi.org/10.1007/3-540-56798-4_140
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-56798-1
Online ISBN: 978-3-540-47741-9
eBook Packages: Springer Book Archive