Skip to main content
SpringerLink
Log in

Some sufficient conditions for 4-regular graphs to have 3-regular subgraphs

  • Graphs and Codes
  • Conference paper
  • First Online:
Algebraic Coding (Algebraic Coding 1993)

Part of the book series: Lecture Notes in Computer Science ((LNCS,volume 781))

Included in the following conference series:

Abstract

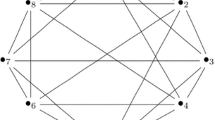
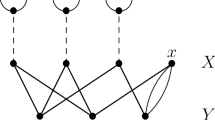
We are interested in the following problem: when would a 4-regular graph (with multiple edges) have a 3-regular subgraph. We give several sufficient conditions for 4-regular graph to have a 3-regular subgraph.

Work partially supported by NSF Grants RII-9014056, the Component IV of the EPSCoR of Puerto Rico Grant, U.S. Army Center of Excellence for Symbolic Methods in Algorithmic Mathematics (ACSyAM), of Cornell MSI. Contract DAAL03-91-C-0027, and the Office of Naval Research under grant number N00014-90-F-1301.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution

Institutional subscriptions

Preview

Unable to display preview. Download preview PDF.

Unable to display preview. Download preview PDF.

References

  1. N. Alon, personal communication, 1993.

    Google Scholar 

  2. N. Alon, S. Friedland and G. Kalai, “Every 4-regular graph plus an edge contains a 3-regular subgraph”, J. Combin. Theory Ser. B 37 (1984), pp 92–93.

    Google Scholar 

  3. N. Alon, S. Friedland and G. Kalai, “Regular subgraphs of almost regular graphs”, J. Combin. Theory Ser. B 37 (1984), pp 79–91.

    Google Scholar 

  4. J. A. Bondy and U. S. R. Murty, Graph Theory with Applications, p. 246, Macmillan and Co., London, 1976.

    Google Scholar 

  5. V. Chvatal, H. Fleischner, J. Sheehan and C. Thomassen, “Three regular subgraphs of four regular graphs”, J. Graph Theory, 3 (1979), pp 371–386.

    Google Scholar 

  6. H. Fleischner, “Eulerian Graphs”, Selected Topics in Graph Theory 2, pp. 17–53, edited by L. W. Beineke and R. J. Wilson, Academic Press, London, 1983.

    Google Scholar 

  7. O. Moreno V. A. Zinoviev, “3-Regular subgraphs of 4-regular graphs”, submitted to J. Combin. Theory Ser. B.

    Google Scholar 

  8. Charles Small, Arithmetic of Finite Fields, pp 50–51, Marcel Dekker Inc., New York, 1991.

    Google Scholar 

  9. V. A. Tâskinov, “Regular subgraphs of regular graphs”, Soviet Math. Dokl., 26 (1982), pp 37–38.

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, University of Puerto Rico, 00931, Rio Piedras, P.R., USA

    Oscar Moreno & Victor A. Zinoviev

  2. Institute for Problems of Information Transmission Russian Academy of Sciences, Ermolova str.19, GSP-4, 101447, Moscow, Russia

    Victor A. Zinoviev

Authors
  1. Oscar Moreno
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Victor A. Zinoviev
    View author publications

    You can also search for this author in PubMed Google Scholar

Editor information

G. Cohen S. Litsyn A. Lobstein G. Zémor

Rights and permissions

Reprints and permissions

Copyright information

© 1994 Springer-Verlag Berlin Heidelberg

About this paper

Cite this paper

Moreno, O., Zinoviev, V.A. (1994). Some sufficient conditions for 4-regular graphs to have 3-regular subgraphs. In: Cohen, G., Litsyn, S., Lobstein, A., Zémor, G. (eds) Algebraic Coding. Algebraic Coding 1993. Lecture Notes in Computer Science, vol 781. Springer, Berlin, Heidelberg. https://doi.org/10.1007/3-540-57843-9_18

Download citation

  • DOI: https://doi.org/10.1007/3-540-57843-9_18

  • Published:

  • Publisher Name: Springer, Berlin, Heidelberg

  • Print ISBN: 978-3-540-57843-7

  • Online ISBN: 978-3-540-48357-1

  • eBook Packages: Springer Book Archive

Publish with us

Policies and ethics

Search

Navigation