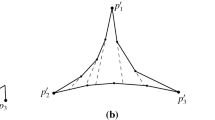
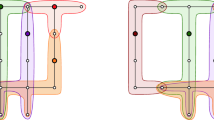
Abstract
We show that the line sweep approach to Voronoi diagrams can be generalized to a very general class of distance measures called nice metrics. This class is more general than the previously studied convex distance functions. It includes e.g the Moscow metric.
We provide the first worst-case optimal algorithm for the full class of nice metrics in the plane. It is conceptually simple and easy to implement, and it copes with all possible deformations of the diagram.
Research partially supported by the Natural Sciences and Engineering Research Council of Canada.
Research partially supported by the Deutsche Forschungsgemeinschaft, grant no. Kl 655–2.
This is a preview of subscription content, log in via an institution to check access.
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
M. Atallah: Dynamic computational geometry. Comput. Math. Appl. 11, pages 1171–1181, 1985.
F. Aurenhammer: Voronoi diagrams — A survey of a fundamental data structure. ACM Computer Surveys 23 (3), 1991.
K. Q. Brown: Voronoi diagrams from convex hulls. Inf. Process. Lett. 9 (5), pages 223–228, 1979.
K. L. Clarkson and P. W. Shor: Applications of random sampling in computational geometry, II. Discrete. Comput. Geom. 4, pages 387–421, 1989.
L. P. Chew and R. L. Drysdale III: Voronoi diagrams based on convex distance functions. In Proceedings 1st ACM Symposium on Computational Geometry, 1985, pages 235–244.
R. Cole: Reported by C. Ó'Dúnlaing, 1989.
F. Dehne and R. Klein: A sweepcircle algorithm for Voronoi diagrams. In H. Göttler and H. J. Schneider, editors, Graphtheoretic concepts in Computer Science (WG '87), pages 59–70, Staffelstein. LNCS 314, Springer-Verlag, Berlin, 1988.
H. Edelsbrunner and R. Seidel: Voronoi diagrams and arrangements. Discrete Comput. Geom. 1, pages 25–44, 1986.
S. Fortune: A sweepline algorithm for Voronoi diagrams. Algorithmica, 2 (2), pages 153–174, 1987.
R. Klein: Concrete and abstract Voronoi diagrams. LNCS 400, Springer-Verlag, Berlin, 1989.
R. Klein, K. Mehlhorn, and St. Meiser: Randomized Incremental Construction of Abstract Voronoi Diagrams. Computational Geometry: Theory and Applications 3 (1993), pp. 157–184.
A. G. Corbalan, M. L. Mazón and T. Recio: About the Voronoi diagrams for strictly convex distances. Manuscript, Departamento De Matemáticas, Universidad de Cantabria, Santander, España, 1991.
R. Seidel: Constrained Delaunay triangulations and Voronoi diagrams with obstacles. Technical Report 260, IIG-TU Graz, Austria, pages 178–191, 1988.
M. I. Shamos and D. Hoey: Closest-point problems. In Proceedings 16th IEEE Symposium on Foundations of Computer Science, 1975, pages 151–162.
G. M. Shute, L. L. Deneen, and C. D. Thomborson: An O(n log n) plane-sweep algorithm for L 1 and L ∞ Delaunay triangulations. Algorithmica 6(2), 1991, pages 207–221.
S. Skyum: A sweepline algorithm for generalized Delaunauy triangulations. Tech. Rep. DAIMI PB — 373, CS Dept., Aarhus Univ., Nov. 1991.
Author information
Authors and Affiliations
Editor information
Rights and permissions
Copyright information
© 1994 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Dehne, F., Klein, R. (1994). “The big sweep”: On the power of the wavefront approach to Voronoi diagrams. In: Prívara, I., Rovan, B., Ruzička, P. (eds) Mathematical Foundations of Computer Science 1994. MFCS 1994. Lecture Notes in Computer Science, vol 841. Springer, Berlin, Heidelberg. https://doi.org/10.1007/3-540-58338-6_76
Download citation
DOI: https://doi.org/10.1007/3-540-58338-6_76
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-58338-7
Online ISBN: 978-3-540-48663-3
eBook Packages: Springer Book Archive