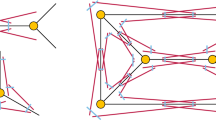
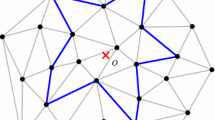
Abstract
For a polygon P, the skeleton of P is a partition of P into regions assigned to the edges of P. A point p inside P belongs to the region of an edge e if and only if e is the closest edge of P. We present a randomized algorithm that builds the skeleton of a simple polygon in linear expected time. We also observe that the Delaunay triangulation (equivalently, the Voronoi diagram) of a planar point set can be computed from its connected spanning subgraph in linear expected time.
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
A. Aggarwal, L.J. Guibas, J. Saxe, and P.W. Shor. A Linear-Time Algorithm for Computing the Voronoi Diagram of a Convex Polygon. Discrete and Computational Geometry 4, 1987.
F. Aurenhammer. Voronoi Diagrams—A Survey of a Fundamental Geometric Data Structure. ACM Computing Surveys 23, 1991, pp. 345–405.
B. Chazelle. Triangulating a Simple Polygon in Linear Time. Discrete and Computational Geometry 6, 1991, pp. 485–524.
P. Chew. Building Voronoi Diagrams for Convex Polygons in Linear Expected Time. Manuscript, 1986.
P. Chew. Constrained Delaunay Triangulations Proc. 3rd ACM Symposium on Computational Geometry, 1987, pp. 215–222.
K.L. Clarkson, K. Mehlhorn and R. Seidel. Four results on randomized incremental constructions. Computational Geometry: Theory and Applications 3 (1993), pp. 185–212.
O. Devillers. Randomization yields simple O(n log* n) algorithms for difficult Ω(n) problems. International Journal of Computational Geometry and Applications, Vol2, No1 (1992), pp. 97–111
H. Djidjev and A. Lingas. On Computing the Voronoi Diagram for Restricted Planar Figures. Proc. WADS'91, LNCS 519, pp. 54–64, Springer Verlag. To appear in International Journal of Computational Geometry and Applications.
R.L. Graham and F.F. Yao. Finding the convex hull of a simple polygon. J. Algorithms 4(4), pp. 324–331, 1983.
M. Held. On the Computational Geometry of Pocket Machining. LNCS 500, Springer-Verlag, 1991.
D.G. Kirkpatrick. Efficient computation of continuous skeletons. Proceedings of the 20th FOCS, pp. 18–27.
R. Klein, K. Mehlhorn, and S. Meiser. Randomized Incremental Construction of Abstract Voronoi Diagrams. Computational Geometry: Theory and Applications 3 (1993), pp. 157–184.
R. Klein and A. Lingas. A Linear-Time Randomized Algorithm for the Bounded Voronoi Diagram of a Simple Polygon. 9th ACM Symposium on Computational Geometry, San Diego, U.S.A., 1993, pp. 124–132.
R. Klein and A. Lingas. A Note on Generalizations of Chew's Algorithm for the Voronoi Diagram of a Convex Polygon. Proc. 5CCCG, pp. 370–374, 1993.
R. Klein and A. Lingas. Hamiltonian Abstract Voronoi Diagrams in Linear Time. Proc. ISAAC'94, LNCS, Springer Verlag.
D.T. Lee. On finding the convex hull of a simple polygon. Int'l J. Comput. and Infor. Sci. 12(2), 87–98, 1983.
D.T. Lee and A. Lin. Generalized Delaunay Triangulations for Planar Graphs. Discrete and Computational Geometry 1, 1986, pp. 201–217.
A. Lingas. Voronoi Diagrams with Barriers and the Shortest Diagonal Problem. Information Processing Letters 32, 1989, pp. 191–198.
U. Montanari. Continuous Skeletons from Digitized Images. J. ACM 16 (1969) pp. 564–549.
A. Okabe, B. Boots, and K. Sugihara. Spatial Tessellations, Concepts and Applications of Voronoi Diagrams. John Wiley & Sons, West Sussex, 1992.
F.P. Preparata and M.I. Shamos. Computational Geometry: An Introduction. Texts and Monographs in Theoretical Computer Science, Springer Verlag, New York, 1985.
R. Seidel. Constrained Delaunay triangulations and Voronoi diagrams with obstacles. In Rep. 260, IIG-TU Graz, Austria, pp. 178–191.
R. Seidel. Backwards Analysis of Randomized Geometric Algorithms. New Trends in Discrete and Computational Geometry, Janos Pach (ed.), Springer-Verlag, 1993.
R. Seidel. A simple and fast incremental and randomized algorithms for computing trapezoidal decompositions and for triangulating polygons. Computational Geometry: Theory and Applications, vol. 1, no. 1, 1991.
C. Wang and L. Schubert. An Optimal Algorithm for Constructing the Delaunay Triangulation of a Set of Line Segments. Proc. 3rd ACM Symposium on Computational Geometry, Waterloo, pp. 223–232, 1987.
C. Yap. An O(n log n) algorithm for the Voronoi diagram of a set of simple curve segments. Discrete Computational Geometry 2 (1987), pp. 365–393.
C. Yap and H. Alt Motion Planning in the CL-Environment. Proc. WADS'89, Ottawa, Canada, LNCS 382, pp. 373–380.
Author information
Authors and Affiliations
Editor information
Rights and permissions
Copyright information
© 1995 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Klein, R., Lingas, A. (1995). Fast skeleton construction. In: Spirakis, P. (eds) Algorithms — ESA '95. ESA 1995. Lecture Notes in Computer Science, vol 979. Springer, Berlin, Heidelberg. https://doi.org/10.1007/3-540-60313-1_172
Download citation
DOI: https://doi.org/10.1007/3-540-60313-1_172
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-60313-9
Online ISBN: 978-3-540-44913-3
eBook Packages: Springer Book Archive