Abstract
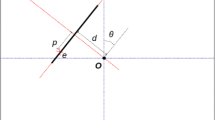
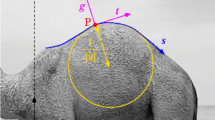
The Hough transform is a standard technique for finding features such as lines in images. Typically, points or edgels are mapped into a partitioned parameter or Hough space as individual votes where peaks denote the feature of interest. The standard mapping used for line detection is the Rθ mapping and the key property the Hough transform exploits is that lines in the image map to points in Hough space. In this paper we introduce and explore three further properties of the Rθ mapping and suggest applications for them. Firstly, we show that points in Hough space with maximal R forany value of θ are on the convex hull of the object in image space. It is shown that approximate hulls of 2D and 3D hulls of objects can be constructed in linear time using this approach. Secondly, it is shown that a simple relationship exists between the occluding contour of an object and the Rθ mapping and that this could in principle be used to generate approximate aspect graphs of objects whose geometry was known. Thirdly, it is shown that antipodal points on object boundaries, (which are optimal robot grasp points), can be found by translation and reflection of the Rθ representation.In addition we show the relationship between the Rθ mapping used in the Hough transform and the classical mathematical theory of duals. We use this analysis to prove formally stated properties of the Rθ mapping from image space to Hough space and in particular the relationship to the convex hull.
This work was funded by EPSRC grant number GR/J44018
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
A. Blake. A theory of planar grasp. OUEL Report 1958/92, Oxford University Engineering Department, October 1992.
J. W. Bruce. The duals of generic hypersurfaces. Math. Scand, 49:36–69, 1981.
J.W Bruce and P.J. Giblin. Curves and singularities. Cambridge University Press, second edition, 1992.
R. L. Graham. An efficient algorithm for determining the convex hull of a finite planar set. Information processing letters, 1:132–133, 1972.
P. V. C. Hough. Method and means for recognising complex patterns. US Patent 3069654, 1962.
J. Illingworth and J. Kittler. A survey of the Hough transform. CVGIP, 44:87–116, 1988.
C. Kimme, D. Ballard, and J. Sklansky. Finding circles by an array of accululators. Comm ACM, 18:120–122, 1975.
J. J. Koenderink. Solid shape. M.I.T Press, 1990.
J. J. Koenderink and A. J. van Doorn. The internal representions of solid shape with respect to vision. Biological Cybernetics, 32:211–216, 1979.
K. Murakami, H. Koshimizu, and K. Hasegawa. An algorithm to extract convex hull on θ–ρ Hough transform space. In 9th International Conference on Pattern Recognition, 1988.
J. O'Rourke. Computational geometry in C. Cambridge University press, 1992.
J. Plucker. System der analytischen geometrie. Berlin, 1835.
J. Plucker. Theorie der algebraischen kurven. Bonn, 1839.
Math Works. MATLAB user guide, 1992.
M. W. Wright, A. Fitzgibbon, P. J. Giblin, and R. B. Fisher. Convex hulls, occluding contours, aspect graphs and the Hough transform. In British Machine Vision Conference, pages 493–502, 1995.
Author information
Authors and Affiliations
Editor information
Rights and permissions
Copyright information
© 1996 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Wright, M., Fitzgibbon, A., Giblin, P.J., Fisher, R.B. (1996). Beyond the Hough transform: Further properties of the Rθ mapping and their applications. In: Ponce, J., Zisserman, A., Hebert, M. (eds) Object Representation in Computer Vision II. ORCV 1996. Lecture Notes in Computer Science, vol 1144. Springer, Berlin, Heidelberg. https://doi.org/10.1007/3-540-61750-7_37
Download citation
DOI: https://doi.org/10.1007/3-540-61750-7_37
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-61750-1
Online ISBN: 978-3-540-70673-1
eBook Packages: Springer Book Archive