Abstract
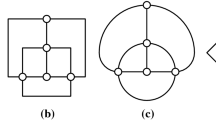
We investigate the problem of drawing an arbitrary n-node binary tree orthogonally in an integer grid using straight-line edges. We show that one can simultaneously achieve good area bounds while also allowing the aspect ratio to be chosen as being O(1) or sometimes even an arbitrary parameter. In addition, we show that one can also achieve an additional desirable aesthetic criterion, which we call “subtree separation.” We investigate both upward and non-upward drawings, achieving area bounds of O(n log n) and O(n log log n), respectively, and we show that, at least in the case of upward drawings, our area bound is optimal to within constant factors.
This work is a consequence of the participation of Drs. Goodrich and Tamassia in the 1996 International Workshop on 3D Graph Drawing at Bellairs Research Inst. of McGill University.
This research was performed while the author was visiting the Center for Geometric Computing at Johns Hopkins University, and it was supported in part by by ARO under grant DAAH04-96-1-0013.
This research supported by NSF under Grants CCR-9300079 and CCR-9625289, and by ARO under grant DAAH04-96-1-0013.
This research supported by NSF under Grant CCR-9508545 and by ARO under grant DAAH04-96-1-0013.
This research supported by NSF under Grant CCR-9423847 and by ARO under grant DAAH04-96-1-0013.
Chapter PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
References
R. P. Brent and H. T. Kung. On the area of binary tree layouts. Inform. Process. Lett., 11:521–534, 1980.
P. Crescenzi, G. Di Battista, and A. Piperno. A note on optimal area algorithms for upward drawings of binary trees. Comput. Geom. Theory Appl., 2:187–200, 1992.
P. Crescenzi and A. Piperno. Optimal-area upward drawings of AVL trees. In R. Tamassia and I. G. Tollis, editors, Graph Drawing (Proc. GD '94), volume 894 of Lecture Notes in Computer Science, pages 307–317. Springer-Verlag, 1995.
G. Di Battista, P. Eades, R. Tamassia, and I. G. Tollis. Algorithms for drawing graphs: an annotated bibliography. Comput. Geom. Theory Appl., 4:235–282, 1994.
A. Garg, M. T. Goodrich, and R. Tamassia. Area-efficient upward tree drawings. In Proc. 9th Annu. ACM Sympos. Comput. Geom., pages 359–368, 1993.
C. E. Leiserson. Area-efficient graph layouts (for VLSI). In Proc. 21st Annu. IEEE Sympos. Found. Comput. Sci., pages 270–281, 1980.
C. E. Leiserson. Area-efficient graph layouts (for VLSI). ACM Doctoral Dissertation Award Series. MIT Press, Cambridge, MA, 1983.
E. Reingold and J. Tilford. Tidier drawing of trees. IEEE Trans. Softw. Eng., SE-7(2):223–228, 1981.
Y. Shiloach. Arrangements of Planar Graphs on the Planar Lattice. PhD thesis, Weizmann Institute of Science, 1976.
L. Trevisan. A note on minimum-area upward drawing of complete and Fibonacci trees. Information Processing Letters, 57(5):231–236, 1996.
L. Valiant. Universality considerations in VLSI circuits. IEEE Trans. Comput., C-30(2):135–140, 1981.
Author information
Authors and Affiliations
Editor information
Rights and permissions
Copyright information
© 1997 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Chan, T., Kosaraju, S.R., Goodrich, M.T., Tamassia, R. (1997). Optimizing area and aspect ratio in straight-line orthogonal tree drawings. In: North, S. (eds) Graph Drawing. GD 1996. Lecture Notes in Computer Science, vol 1190. Springer, Berlin, Heidelberg. https://doi.org/10.1007/3-540-62495-3_38
Download citation
DOI: https://doi.org/10.1007/3-540-62495-3_38
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-62495-0
Online ISBN: 978-3-540-68048-2
eBook Packages: Springer Book Archive