Abstract
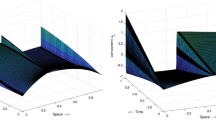
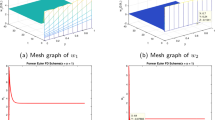
A numerical method is developed for a time dependent reaction diffusion two dimensional problem. This method is deduced by combining an alternating direction technique and the central finite difference scheme on some special piecewise uniform meshes. We prove that this method is uniformly convergent with respect to the diffusion parameter ε, achieving order 1 in both spatial and time variables. The theoretical results are confirmed by the numerical experiences performed.
This research has been partially supported by the CICYT project. num. AMB94-0396 and by a project of Gobierno de Navarra
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
Clavero, C., Jorge, J.C., Lisbona, F.: Uniformly convergent schemes for singular perturbation problems combining alternating directions and exponential fitting techniques. In Applications of Avanced Computational Methods for Boundary and Interior Layers (J.J.H. Miller, Ed). Boole Press. Dublin (1993) 33–52
Farrell, P.A.: Sufficient conditions for uniform convergence of a class of difference schemes for a singularly perturbed problem. IMA J. Numer. Anal. 7 (1987) 459–472
Hegarty, A.F., Miller, J.J.H., O'Riordan, E., Shishkin, G.I.: Special numerical methods for convection-dominated laminar flows at arbitrary Reynolds number. East-West J. Numer. Math. 2 (1994) 65–74
Hegarty, A.F., Miller, J.J.H., O'Riordan, E., Shishkin, G.I.: Special meshes for finite difference approximations to an advection-diffusion equation with parabolic layers. J. Comp. Phys. 117 (1995) 47–54
Herceg, D.: Uniform fourth order difference scheme for a singular perturbation problem. Numer. Math. 56 (1990) 675–693
Jorge, J. C., Lisbona, F.: Contractivity results for alternating direction schemes in Hilbert spaces. App. Numer. Math. 15 (1994) 65–75
Kellogg, R.B., Tsan, A.: Analysis of some difference approximations for a singular perturbation problem without turning points. Math. Comp. 32 (1978) 1025–1039
Shishkin, G.I.: Grid pproximation of singularly perturbed boundary value problems with convective terms. Sov. J. Numer. Anal. Math. Modelling 5 (1990) 173–187
Shishkin, G.I.: Grid approximations of singularly perturbed elliptic and parabolic equations (in Russian). Russian Academy Science, Ural Branch, Ekaterinburg (1992)
Stynes M., Roos, H.G.: The Midpoint Upwind Scheme. Preprint of Dep. of Math., University College, Cork (1996)
Author information
Authors and Affiliations
Editor information
Rights and permissions
Copyright information
© 1997 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Clavero, C., Jorge, J.C., Lisbona, F., Shishkin, G.I. (1997). Splitting time methods and one dimensional special meshes for reaction-diffusion parabolic problems. In: Vulkov, L., Waśniewski, J., Yalamov, P. (eds) Numerical Analysis and Its Applications. WNAA 1996. Lecture Notes in Computer Science, vol 1196. Springer, Berlin, Heidelberg. https://doi.org/10.1007/3-540-62598-4_84
Download citation
DOI: https://doi.org/10.1007/3-540-62598-4_84
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-62598-8
Online ISBN: 978-3-540-68326-1
eBook Packages: Springer Book Archive