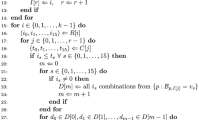Abstract
Boolean functions are basic building blocks of virtually any cipher. Tremendous amount of research is devoted to finding Boolean functions that would be best suited for the job. A number of cryptographic criteria have been proposed that a Boolean function should fulfill to be considered for use in a cipher system. Most of these criteria in one way or another are correlated with function’s nonlinearity. Also a number of specific algebraic constructions and algorithms have been developed that allow us to obtain such Boolean functions with those desirable properties. Efficient representation and implementation of such cipher systems is another challenge faced by today’s cryptologists. This article presents a simple algorithm that is able to randomly generate Boolean functions with surprisingly good cryptographic properties, which at the same time have extremely short ANF representation, which could lead to efficient implementations.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
C. M. Adams, S. E. Tavares. Generating and Counting Binary Bent Sequences. In IEEE Transactions on Information Theory, IT-36:1170–1173, 1990.
J. A. Clark, J. L. Jacob, S. Stepney. Searching for cost functions. In CEC 2004: International Conference on Evolutionary Computation, Portland OR, USA, June 2004, pages 1517–1524, IEEE 2004.
J. Fuller, W. Millan. On Linear Redundancy in the AES S-box. In Cryptology ePrint Archive, report 2002/111 , eprint.iacr.org, Aug 2002.
J. Fuller, W. Millan. Linear Redundancy in S-Boxes. In T. Johansson, editor, February 24-26, 2003. Revised Papers, volume 2887 of Lecture Notes in Computer Science, pages 74–86, 2003.
X. Guo-Zhen, J. Massey. A spectral characterization of correlation immune combining functions. In IEEE Transactions on Information Theory, 34(3):569–571, May 1988.
X. D. Hou. On the norm and covering radius of first-order Reed-Muller codes. In IEEE Transactions on Information Theory, 43(3):1025–1027, May 1997.
J. B. Kam, G. Davida. Structured Design of Substitution-Permutation Encryption Networks. In IEEE Transactions on Computers, C-28:747–753, 1979.
J. A. Maiorana A Class of Bent Functions. In R41 Technical Paper, 1971.
W. Meier, O. Staffelbach. Nonlinearity criteria for cryptographic functions. In J. J. Quisquater, J. Vandewalle, editors, Advances in Cryptology: EUROCRYPT 1989, pages 549–562, LNCS 434, Springer, 1989.
W. Millan, A. Clark, E. Dawson. Heuristic design of cryptographically strong balanced Boolean functions. In Advances in Cryptology: EUROCRYPT 1998, pages 489–499, LNCS 1403, Springer, 1998.
O. S. Rothaus. On bent functions. In Journal of Combinatorial Theory: Series A, 20:300–305, 1976.
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2007 Springer Science+Business Media, LLC
About this paper
Cite this paper
Czurylo, A.G. (2007). Strong Boolean Functions with Compact ANF Representation. In: Pejaś, J., Saeed, K. (eds) Advances in Information Processing and Protection. Springer, Boston, MA. https://doi.org/10.1007/978-0-387-73137-7_19
Download citation
DOI: https://doi.org/10.1007/978-0-387-73137-7_19
Publisher Name: Springer, Boston, MA
Print ISBN: 978-0-387-73136-0
Online ISBN: 978-0-387-73137-7
eBook Packages: Computer ScienceComputer Science (R0)