Skip to main content
SpringerLink
Log in

Lagrangian Duality: BASICS

  • Reference work entry
Book cover Encyclopedia of Optimization

Article Outline

Keywords

The Primal Problem and the Lagrangian Dual Problem

Weak and Strong Duality

Properties of the Lagrangian Dual Function

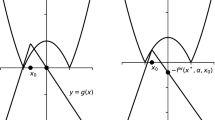
Geometrical Interpretations of Lagrangian Duality

  The Resource-Payoff Space

  Gap Function

Summary

See also

References

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution
Chapter
USD 29.95
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever
eBook
USD 2,500.00
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever
Hardcover Book
USD 2,499.99
Price excludes VAT (USA)
  • Durable hardcover edition
  • Dispatched in 3 to 5 business days
  • Free shipping worldwide - see info

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

References

  1. Balinski ML, Baumol WJ (1968) The dual in nonlinear programming and its economic interpretation. Rev Economic Stud 35:237–256

    Article  MATH  Google Scholar 

  2. Bazaraa MS, Goode JJ (1979) A survey of various tactics for generating Lagrangian multipliers in the context of Lagrangian duality. Europ J Oper Res 3:322–338

    Article  MathSciNet  MATH  Google Scholar 

  3. Bertsekas DP (1975) Nondifferentiable optimization. North-Holland, Amsterdam

    Google Scholar 

  4. Bertsekas DP (1982) Constrained optimization and Lagrange multiplier methods. Acad. Press, New York

    MATH  Google Scholar 

  5. Bertsekas DP (1995) Nonlinear programming. Athena Sci., Belmont, MA

    MATH  Google Scholar 

  6. Brooks R, Geoffrion A (1966) Finding Everett's Lagrange multipliers by linear programming. Oper Res 16:1149–1152

    MathSciNet  Google Scholar 

  7. Everett H (1973) Generalized Lagrange multiplier method for solving problems of optimum allocation of resources. Oper Res 4:72–97

    Google Scholar 

  8. Falk JE (1967) Lagrange multipliers and nonconvex programming. J Math Anal Appl 19:141–159

    Article  MathSciNet  MATH  Google Scholar 

  9. Fiacco AV, McCormick GP (1968) Nonlinear programming: Sequential unconstrained minimization techniques. Wiley, New York

    MATH  Google Scholar 

  10. Fisher ML, Northup WD, Shapiro JF (1975) Using duality to solve discrete optimization problems: theory and computational experience. In: Balinski ML, Wolfe P (eds) Nondifferentiable Optimization. North-Holland, Amsterdam

    Google Scholar 

  11. Fletcher R (ed) (1969) Optimization. Acad. Press, New York

    MATH  Google Scholar 

  12. Geoffrion AM (1970) Elements of large- scale mathematical programming I-II. Managem Sci 16:652–675; 676–691

    MathSciNet  Google Scholar 

  13. Geoffrion AM (1971) Duality in nonlinear programming: A simplified application-oriented development. SIAM Rev 13:1–7

    Article  MathSciNet  MATH  Google Scholar 

  14. Hearn DW (1982) The gap function of a convex program. Oper Res Lett 1:67–71

    Article  MathSciNet  MATH  Google Scholar 

  15. Hearn DW, Lawphongpanich S (1989) Lagrangian dual ascent by generalized linear programming. Oper Res Lett 8:189–196

    Article  MathSciNet  MATH  Google Scholar 

  16. Hearn DW, Lawphongpanich S (1990) A dual ascent algorithm for traffic assignment problems. Transport Res B 248(6):423–430

    Article  MathSciNet  Google Scholar 

  17. Kiwiel KC (1985) Methods of descent for nondifferentiable optimization. Springer, Berlin

    MATH  Google Scholar 

  18. Lasdon LS (1970) Optimization theory for large systems. MacMillan, New York

    MATH  Google Scholar 

  19. Luenberger DG (1969) Optimization by vector space methods. Wiley, New York

    MATH  Google Scholar 

  20. Luenberger DG (1973) Introduction to linear and nonlinear programming. Addison-Wesley, Reading, MA

    MATH  Google Scholar 

  21. Mangasarian OL (1969) Nonlinear programming. McGraw-Hill, New York

    MATH  Google Scholar 

  22. Nemhauser GL, Wolsey LA (1988) Integer and combinatorial optimization. Wiley, New York

    MATH  Google Scholar 

  23. Powell MJD (1978) Algorithms for nonlinear constraints that use Lagrangian functions. Math Program 14:224–248

    Article  MathSciNet  MATH  Google Scholar 

  24. Rockafellar RT (1970) Convex analysis. Princeton Univ. Press, Princeton

    MATH  Google Scholar 

  25. Rockafellar RT (1975) Lagrange multipliers in optimization. In: Cottle RW, Lemke CE (eds) Nonlinear Programming, SIAM-AMS Proc. vol IX, pp 23–24

    Google Scholar 

  26. Whittle P (1971) Optimization under constraints. Wiley, New York

    MATH  Google Scholar 

  27. Wolfe P (1961) A duality theorem for nonlinear programming. Quart Appl Math 19:239–244

    MathSciNet  MATH  Google Scholar 

  28. Zangwill WI (1969) Nonlinear programming: A unified approach. Prentice-Hall, Englewood Cliffs, NJ

    MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. University Florida, Gainesville, USA

    Donald W. Hearn

  2. University Iowa, Iowa City, USA

    Timothy J. Lowe

Authors
  1. Donald W. Hearn
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Timothy J. Lowe
    View author publications

    You can also search for this author in PubMed Google Scholar

Editor information

Editors and Affiliations

  1. Department of Chemical Engineering, Princeton University, Princeton, NJ, 08544-5263, USA

    Christodoulos A. Floudas

  2. Center for Applied Optimization, Department of Industrial and Systems Engineering, University of Florida, Gainesville, FL, 32611-6595, USA

    Panos M. Pardalos

Rights and permissions

Reprints and permissions

Copyright information

© 2008 Springer-Verlag

About this entry

Cite this entry

Hearn, D.W., Lowe, T.J. (2008). Lagrangian Duality: BASICS . In: Floudas, C., Pardalos, P. (eds) Encyclopedia of Optimization. Springer, Boston, MA. https://doi.org/10.1007/978-0-387-74759-0_320

Download citation

Publish with us

Policies and ethics

Search

Navigation