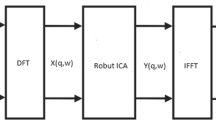
We consider the problem of convolutive blind source separation (BSS). This is usually tackled through either multichannel blind deconvolution (MCBD) or using frequency-domain independent component analysis (FD-ICA). Here, instead of using a fixed time or frequency basis to solve the convolutive blind source separation problem we propose learning an adaptive spatial–temporal transform directly from the speech mixture. Most of the learnt space–time basis vectors exhibit properties suggesting that they represent the components of individual sources as they are observed at the microphones. Source separation can then be performed by projection onto the appropriate group of basis vectors.We go on to show that both MCBD and FD-ICA techniques can be considered as particular forms of this general separation method with certain constraints. While our space–time approach involves considerable additional computation it is also enlightening as to the nature of the problem and has the potential for performance benefits in terms of separation and de-noising.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
S.-I. Amari, S. Douglas, A. Cichocki, and H. Yang, “Multichannel blind decon-volution and equalization using the natural gradient,” in Proc. IEEE Workshop on Signal Processing Advances in Wireless Communications, Apr. 1997, pp. 101-104.
K. Torkkola, “Blind separation of convolved sources based on information max-imization,” in Proc. of the IEEE Workshop on Neural Networks for Signal Processing (NNSP), 1996, pp. 423-432.
S. C. Douglas and X. Sun, “Convolutive blind separation of speech mixtures using the natural gradient,” Speech Communication, vol. 39, pp. 65-78, 2003.
S. Makino, H. Sawada, R. Mukai, and S. Araki, “Blind source separation of con-volutive mixtures of speech in frequency domain,” IEICE Trans. Fundamentals vol. E88, pp. 1640-1655, 2005.
S. Adballah and M. Plumbley, “Application of geometric dependency analysis to the separation of convolved mixtures,” in Proc. ICA 2004 (LNCS 3195), Sept. 2004, pp. 540-547.
M. G. Jafari, S. A. Abdallah, M. D. Plumbley, and M. E. Davies, “Sparse coding for convolutive blind audio separation,” in Proc. ICA 2006 (LNCS 3889), Mar. 2006, pp. 132-139.
N. Mitianoudis and M. Davies, “Audio source separation of convolutive mix-tures,” IEEE Trans. Audio and Speech Processing, vol. 11, pp. 489-497, 2003.
R. H. Lambert, Multichannel Blind Deconvolution: FIR Matrix Algebra and Separation of Multipath Mixtures, Ph.D. dissertation, University of Southern California, Los Angeles, CA., 1996.
P. Smaragdis, “Blind separation of convolved mixtures in the frequency do-main,” Neurocomputing, vol. 22, pp. 21-34, 1998.
J.F. Cardoso, “Blind signal separation: statistical principles,” Proceedings of the IEEE, vol. 86, no. 10, pp. 2009-2025, 1998.
S. Araki, S. Makino, R. Aichner, T. Nishikawa, and H. Saruwatari, “Subband based blind source separation with appropriate processing for each frequency band,” in Proc. ICA 2003, Apr. 2003, pp. 499-504.
J.-F. Cardoso and B. Laheld, “Equivariant adaptive source separation,” IEEE Trans. Signal Processing, vol. 44, pp. 3017-3030, 1996.
S. Amari and A. Cichocki, “Adaptive blind signal processing - neural network approaches,” Proceedings of the IEEE, vol. 86, no. 10, pp. 2026-2048, 1998.
A. Hyvärinen, “Fast and robust fixed-point algorithm for independent com-ponent analysis,” IEEE Trans. Neural Networks, vol. 10, no. 3, pp. 626-634, 1999.
S. Ikeda and N. Murata, “A method of ICA in time-frequency domain,” in Proc. ICA99, Jan. 1999, pp. 365-371.
M. E. Davies, “Audio source separation,” in Mathematics of Signal Process-ing V, Eds. J. G. McWhirter and I. K. Proudler, Oxford University Press, 2002, pp. 57-68.
I. Lee, T. Kim, and T.-W. Lee, “Complex FastIVA: A robust maximum likeli-hood approach of MICA for convolutive BSS”, in Proc. ICA 2006 (LNCS 3889), Mar. 2006, pp. 625-632.
S. Araki, S. Makino, R. Mukai, Y. Hinamoto, T. Nishikawa, and H. Saruwatari, “Equivalence between frequency domain blind source separation and fre-quency domain adaptive beamforming,” in Proc. ICASSP 2002, May 2002, pp. 1785-1788.
S. Kurita, H. Saruwatari, S. Kajita K. Takeda, and F. Itakura, “Evaluation of blind signal separation method using directivity pattern under reverberant conditions,” in Proc. ICASSP 2000, June 2000, pp. 3140-3143.
H. Saruwatari, S. Kurita, and K. Takeda, “Blind source separation combining frequency-domain ICA and beamforming,” in Proc. ICASSP 2001, May 2001, pp. 2733-2736.
M. Z. Ikram and D. R. Morgan, “A beamforming approach to permutation alignment for multichannel frequency-domain blind speech separation,” in Proc. ICASSP 2002, May 2002, pp. 881-884.
H. Sawada, R. Mukai, S. Araki, and S. Makino, “A robust and precise method for solving the permutation problem of frequency-domain blind source separa-tion,” IEEE Trans. Speech and Audio Processing, vol. 12, pp. 530-538, 2004.
S. C. Douglas and S. Haykin, “Relationships between blind deconvolution and blind source separation,” in Unsupervised Adaptive Filtering, vol. 2, Ed. S. Haykin, John Wiley & Sons, 2002, pp. 113-145.
W. L. Melvin, “A STAP overview,” IEEE A&E Systems Magazine, vol. 19, no. 1, pp. 19-35, 2004.
J.-F. Cardoso, “Multidimensional independent component analysis,” in Proc. ICASSP’98, May 1998, pp. 1941-1944.
R. M. Gray, “On the asymptotic eigenvalue distribution of Toeplitz matrices,” IEEE Trans. Info. Theory, vol. IT-18, no. 6, pp. 725-730, 1972.
J. J. Shynk, “Frequency-domain and multirate adaptive filtering,” IEEE Signal Processing Magazine, vol. 9, no. 1, pp. 14-37, Jan. 1992.
A. Bell and T. Sejnowski, “Learning the higher-order structure of a natural sound,” Network: Computation in Neural Systems vol. 7, pp. 261-266, 1996.
A. J. Bell and T. J. Sejnowski, “An information maximization approach to blind separation and blind deconvolution,” Neural Computation, vol. 7, no. 6, pp. 1129-1159, 1995.
B. A. Olshausen and D. J. Field, “Emergence of simple-cell receptive-filed prop-erties by learning a sparse code of natural images,” Nature, vol. 381, pp. 607-609,1996.
S. A. Abdallah and M. D. Plumbley, “If edges are the independent components of natural images, what are the independent components of natural sounds?,” in Proc. ICA 2001, Dec. 2001, pp. 534-539.
M. S. Lewicki, “Efficient coding of natural sounds,” Nature Neuroscience vol. 5, no. 4, pp. 356-363, 2002.
C. Knapp and G. Carter, “The generalized correlation method for estimation of time delay,” IEEE Trans. Acoustic, Speech and Signal Processing, vol. 24, pp. 320-327, 1976.
R. R. Coifman and D. L. Donoho, “Translation-invariant de-noising,” in Wavelets and Statistics, vol. 103, Springer Lecture Notes in Statistics, Eds. A. Antoniadis and G. Oppenheim, Springer-Verlag: New York, 1995, pp. 126-150.
S. McGovern, “A model for room acoustics,” Available at http://2pi.us/rir.html (2003).
N. Mitianoudis and M. Davies, “Permutation alignment for frequency domain ICA using subspace beamforming methods,” in Proc. ICA 2004 (LNCS 3195), Sept. 2004, pp. 669-676.
E. Vincent, R. Gribonval, and C. Févotte, “Performance measurement in blind audio source separation,” IEEE Trans. Audio, Speech and Language Processing vol. 14, no. 4, pp. 1462-1469, 2006.
M. Unser, “On the approximation of the discrete Karhunen-Loeve transform for stationary processes,” Signal Processing, vol. 7, pp 231-249, 1984.
B. D. Van Veen and K. M. Buckley, “Beamforming: a versatile approach to spatial filtering,” IEEE ASSP Magazine, vol. 5, no. 2, pp. 2-24, Apr. 1988.
G. J. Brown, Computational Auditory Scene Analysis: a Representational Approach, Ph.D. dissertation, Computer Science Dept., Sheffield Univ, 1992.
S. Mallat, A Wavelet Tour of Signal Processing, Academic Press, 1999.
A. Hyvärinen, “Sparse code shrinkage: Denoising of nongaussian data by maxi-mum likelihood estimation,” Neural Computation, vol. 11, no. 7, pp. 1739-1768, 1999.
A. Jourjine, S. Rickard, and Ö . Yilmaz, “Blind separation of disjoint orthogonal signals: demixing n sources from 2 mixtures,” in Proc. ICASSP 2000, June 2000, pp. 2985-2988.
M. Casey and A. Westner, “Separation of mixed audio sources by independent subspace analysis,” in Proc. ICMC 2000, Aug. 2000, pp. 154-161.
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2007 Springer
About this chapter
Cite this chapter
Davies, M., Jafari, M., Abdallah, S., Vincent, E., Plumbley, M. (2007). Blind Source Separation using Space–Time Independent Component Analysis. In: Makino, S., Sawada, H., Lee, TW. (eds) Blind Speech Separation. Signals and Communication Technology. Springer, Dordrecht. https://doi.org/10.1007/978-1-4020-6479-1_3
Download citation
DOI: https://doi.org/10.1007/978-1-4020-6479-1_3
Publisher Name: Springer, Dordrecht
Print ISBN: 978-1-4020-6478-4
Online ISBN: 978-1-4020-6479-1
eBook Packages: EngineeringEngineering (R0)