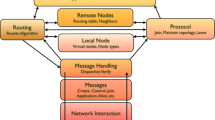
Peer-to-Peer (p2p) algorithms are nowadays standard. However, their specification and verification is not. Currently, the properties that such algorithms should satisfy are stated informally, and the algorithms themselves are often given as pseudo-code. Because of this, no satisfying methods for modeling, specifying and/or verifying these algorithms have yet been developed. We therefore propose a distributed stochastic process calculus to model such algorithms and to formally state and prove relevant functional and performance properties.
This is a preview of subscription content, log in via an institution to check access.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
R. Bakhshi and D. Gurov. Verification of peer-to-peer algorithms: A case study. Electr. Notes Theor. Comput. Sci., 181:35-47, 2007.
J. Borgstr öm, U. Nestmann, L. Onana Alima, and D. Gurov. Verifying a structured peer- to-peer overlay network: The static case. Global Computing, volume 3267 of LNCS, pages 250-265. Springer, 2004.
M. J. Fischer, N. A. Lynch, and M. Paterson. Impossibility of distributed consensus with one faulty process. J. ACM, 32(2):374-382, 1985.
A. Francalanza and M. Hennessy. A fault tolerance bisimulation proof for consensus (extended abstract). ESOP, volume 4421 of LNCS, pages 395-410. Springer, 2007.
N. J. A. Harvey, M. B. Jones, S. Saroiu, M. Theimer, and A. Wolman. Skipnet: A scalable overlay network with practical locality properties. USENIX Symposium on Internet Technologies and Systems, 2003.
M. Hennessy. A Distributed Picalculus. Cambridge University Press, Cambridge, 2007.
H. Hermanns. Interactive Markov Chains: The Quest for Quantified Quality, volume 2428 of LNCS. Springer, 2002.
D. Liben-Nowell, H. Balakrishnan, and D. R. Karger. Analysis of the evolution of peer-to-peer systems. PODC, pages 233-242, 2002.
N. Lynch. Distributed Algorithms. Morgan Kaufmann, San Mateo, CA, 1996.
R. Milner. Communicating and Mobile Systems: The π -Calculus. Cambridge University Press, 1999.
L. Onana Alima, S. El-Ansary, P. Brand, and S. Haridi. DKS (N, k, f): A family of low communication, scalable and fault-tolerant infrastructures for p2p applications. In CCGRID, pages 344-350. IEEE Computer Society, 2003.
A. I. T. Rowstron and P. Druschel. Pastry: Scalable, decentralized object location, and routing for large-scale peer-to-peer systems. Middleware, volume 2218 of LNCS, pages 329-350. Springer, 2001.
I. Stoica, R. Morris, D. Liben-Nowell, D. R. Karger, M. F. Kaashoek, F. Dabek, and H. Balakrishnan. Chord: A scalable peer-to-peer lookup protocol for internet applications. IEEE/ACM Trans. Netw., 11(1):17-32, 2003.
B. Y. Zhao, L. Huang, J. Stribling, S. C. Rhea, A. D. Joseph, and J. Kubiatowicz. Tapestry: A resilient global-scale overlay for service deployment. IEEE Journal on Selected Areas in Communications, 22(1):41-53, 2004.
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2008 Springer Science + Business Media B.V
About this paper
Cite this paper
Schneider, S., Borgström, J., Nestmann, U. (2008). Towards the Application of Process Calculi in the Domain of Peer-to-Peer Algorithms. In: Mahr, B., Huanye, S. (eds) Autonomous Systems – Self-Organization, Management, and Control. Springer, Dordrecht. https://doi.org/10.1007/978-1-4020-8889-6_11
Download citation
DOI: https://doi.org/10.1007/978-1-4020-8889-6_11
Publisher Name: Springer, Dordrecht
Print ISBN: 978-1-4020-8888-9
Online ISBN: 978-1-4020-8889-6
eBook Packages: EngineeringEngineering (R0)