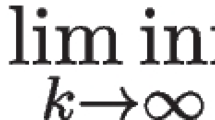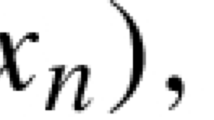Abstract
This is a survey (without proofs except for verifying a few new facts) of the slowest possible rate of convergence of a sequence of linear operators that converges pointwise to a linear operator. A sequence of linear operators (L n ) is said to converge to a linear operator Larbitrarily slowly (resp., almost arbitrarily slowly) provided that (L n ) converges to L pointwise, and for each sequence of real numbers (ϕ(n)) converging to 0, there exists a point x = x ϕ such that \(\|{L}_{n}(x) - L(x)\| \geq \phi (n)\) for all n (resp., for infinitely many n). Two main “lethargy” theorems are prominent in this study, and they have numerous applications. The first lethargy theorem (Theorem 11.16) characterizes almost arbitrarily slow convergence. Applications of this lethargy theorem include the fact that a large class of polynomial operators (e.g., Bernstein, Hermite–Fejer, Landau, Fejer, and Jackson operators) all converge almost arbitrarily slowly to the identity operator. Also all the classical quadrature rules (e.g., the composite Trapezoidal Rule, composite Simpson’s Rule, and Gaussian quadrature) converge almost arbitrarily slowly to the integration functional. The second lethargy theorem (Theorem 11.21) gives useful sufficient conditions that guarantee arbitrarily slow convergence. In the particular case when the sequence of linear operators is generated by the powers of a single linear operator, there is a “dichotomy” theorem (Theorem 11.27) which states that either there is linear (fast) convergence or arbitrarily slow convergence; no other type of convergence is possible. Some applications of the dichotomy theorem include generalizations and sharpening of (1) the von Neumann-Halperin cyclic projections theorem, (2) the rate of convergence for intermittently (i.e., “almost” randomly) ordered projections, and (3) a theorem of Xu and Zikatanov.
AMS 2010 Subject Classification: 40A05, 41A25, 41A36, 41A65, 47N10.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
Amemiya, I., Ando, T.: Convergence of random products of contractions in Hilbert space. Acta Sci. Math. (Szeged) 26, 239–244 (1965)
Aronszajn, N.: Theory of reproducing kernels. Trans. Amer. Math. Soc., 68, 337–403 (1950)
Badea, C., Grivaux, S., Müller, V.: The rate of convergence in the method of alternating projections. St. Petersburg Math. J. 22, (2010). Announced in C. R. Math. Acad. Sci. Paris 348, 53–56 (2010)
Bai, Z.D., Yin, Y.Q.: Necessary and sufficient conditions for almost sure convergence of the largest eigenvalue of a Wigner matrix. Ann. Probability 16, 1729–1741 (1988)
Bauschke, H.H.: A norm convergence result on random products of relaxed projections in Hilbert space. Trans. Amer. Math. Soc. 347, 1365–1373 (1995)
Bauschke, H.H., Borwein, J.M.: On projection algorithms for solving convex feasibility problems. SIAM Review 38, 367–426 (1996)
Bauschke, H.H., Borwein, J.M., Lewis, A.S.: The method of cyclic projections for closed convex sets in Hilbert space. Contemporary Mathematics 204, 1–38 (1997)
Bauschke, H.H., Borwein, J.M., Li, W.: The strong conical hull intersection property, bounded linear regularity, Jameson’s property(G), and error bounds in convex optimization. Math. Programming (Series A) 86, 135–160 (1999)
Bauschke, H.H., Deutsch, F., Hundal, H.: Characterizing arbitrarily slow convergence in the method of alternating projections. Intl. Trans. in Op. Res. 16, 413–425 (2009)
Bernstein, S.N.: On the inverse problem of the theory of the best approximation of continuous functions. Sochineniya II, 292–294 (1938)
Boland, J.M., Nicolaides, R.A.: Stable and semistable low order finite elements for viscous flows. SIAM J. Numer. Anal. 22, 474–492 (1985)
Cheney, W.: Analysis for Applied Mathematics. Graduate Texts in Mathematics #208, Springer, New York (2001)
Combettes, P.L.: Fejér-monotonicity in convex optimization. In: C.A. Floudas and P.M. Pardalos (eds.) Encyclopedia of Optimization, Kluwer Acad. Pub. (2000)
Cover, T.M.: Rates of convergence for nearest neighbor procedures. Proc. Hawaii Intl. Conf. Systems Sciences, 413–415 (1968)
Davis, P.J.: Interpolation and Approximation. Blaisdell, New York (1963)
Deroïan, F.: Formation of social networks and diffusion of innovations. Research Policy 31, 835–846 (2002)
Deutsch, F.: The method of alternating orthogonal projections. In: S.P. Singh (ed.) Approximation Theory, Spline Functions and Applications. Kluwer Academic Publishers, The Netherlands, 105–121 (1992)
Deutsch, F.: The role of the strong conical hull intersection property in convex optimization and approximation. In: C.K. Chui and L.L. Schumaker (eds.) Approximation Theory IX, Vanderbilt University Press, Nashville, TN, 143–150 (1998)
Deutsch, F.: Best Approximation in Inner Product Spaces. Springer, New York (2001)
Deutsch, F., Hundal, H.: Slow convergence of sequences of linear operators I: Almost arbitrarily slow convergence. J. Approx. Theory 162, 1701–1716 (2010)
Deutsch, F., Hundal, H.: Slow convergence of sequences of linear operators II: Arbitrarily slow convergence. J. Approx. Theory 162, 1717–1738 (2010)
Deutsch, F., Ubhaya, V.A., Ward, J.D., Xu, Y.: Constrained best approximation in Hilbert space III. Applications to n-convex functions. Constr. Approx. 12, 361–384 (1996)
Deutsch, F., Li, W., Ward, J.D.: A dual approach to constrained interpolation from a convex subset of Hilbert space. J. Approx. Theory 80, 381–405 (1997)
DeVore, R.: The Approximation of Continuous Functions by Positive Linear Operators. Lecture Notes in Mathematics # 293, Springer, New York (1972)
Devroye, L.: On arbitrarily slow rates of global convergence in density estimation. Probability Theory and Related Fields 62, 475–483 (1983)
Devroye, L.: Another proof of a slow convergence result of Birgé. Statistics and Probability Letters 23, 63–67 (1995)
Devroye, L., Györfi, L., Logosi, G.: A Probabilistic Theory of Pattern Recognition. Springer, New York (1996)
Dye, J., Khamsi, M.A., Reich, S.: Random products of contractions in Banach spaces. Trans. Amer. Math. Soc. 325, 87–99 (1991)
Ghosal, S.: Convergence rates for density estimation with Bernstein polynomials. Ann. Statistics 29, 1264–1280 (2001)
Golightly, A., Wilkinson, D.J.: Bayesian inference for nonlinear multivariate diffusion models observed with error. Computational Statistics and Data Analysis 52, 1674–1693 (2008)
Gordon, R., Bender, R., Herman, G.T.: Algebraic reconstruction techniques (ART) for three-dimensional electron microscopy and X-ray photography. J. Theoretical Biol. 29, 471–481 (1970)
Halperin, I.: The product of projection operators. Acta Sci. Math. (Szeged) 23, 96–99 (1962)
Hanke, M., Neubauer, A., Scherzer, O.: A convergence analysis of the Landweber iteration for nonlinear ill-posed problems. Numerische Math. 72, 21–37 (1995)
Hewitt, E., Stromberg, K.: Real and Abstract Analysis. Springer, New York, (1965)
Hounsfield, G.N.: Computerized transverse axial scanning (tomography); Part I Description of system. British J. Radiol. 46, 1016–1022 (1973)
Hundal, H., Deutsch, F.: Two generalizations of Dykstra’s cyclic projections algorithm. Math. Programming 77, 335–355 (1997)
Jahnke, H.N. (ed.): A History of Analysis. History of Mathematics 24. Amer. Math. Soc., Providence, RI, London Math. Soc., London (2003)
Kincaid, D., Cheney, W.: Numerical Analysis, 2nd edn. Brooks/Cole, New York (1996)
Korovkin, P.P.: Linear Operators and Approximation Theory. Hindustan Publ. Corp. (India), Delhi (1960)
Müller, V.: Power bounded operators and supercyclic vectors II. Proc.Amer. Math. Soc. 133, 2997–3004 (2005)
Müller, V.: Spectral Theory of Linear Operators and Spectral Systems in Banach Algebras, 2nd edn. Operator Theory: Advances and Applications 139, Birkhauser, Basel (2007)
Nakano, H.: Spectal Theory in the Hilbert Space. Japan Soc. Promotion Sc., Tokyo (1953)
Neubauer, A.: On converse and saturation results for Tikhhonov regularization of linear ill-posed problems. SIAM J. Numer. Anal. 34, 517–527 (1997)
von Neumann, J.: On rings of operators. Reduction theory. Ann. of Math. 50, 401–485 (1949)
von Neumann, J.: Functional Operators-Vol. II. The Geometry of Orthogonal Spaces. Annals of Math. Studies #22, Princeton University Press, Princeton, NJ (1950) [This is a reprint of mimeographed lecture notes first distributed in 1933.]
Olshevsky, A., Tsitsiklis, J.N.: Convergence rates in distributed consensus and averaging. Proc. IEEE Conf. Decision Control, San Diego, CA, 3387–3392 (2006)
Powell, M.J.D.: A new algorithm for unconstrained optimization. In: J.B. Rosen, O.L. Mangasarian, and K. Ritter (eds.) Nonlinear Programming, Academic, New York (1970)
Ratschek, H., Rokne, J.G.: Efficiency of a global optimization algorithm. SIAM J. Numer. Anal. 24, 1191–1201 (1987)
Rhee, W., Talagrand, M.: Bad rates of convergence for the central limit theorem in Hilbert space. Ann. Prob. 12, 843–850 (1984)
Schock, E.: Arbitrarily slow convergence, uniform convergence and superconvergence of Galerkin-like methods. IMA Jour. Numerical Anal. 5, 153–160 (1985)
Schock, E.: Semi-iterative methods for the approximated solutions of ill-posed problems. Numer. Math. 50, 263–271 (1987)
Timan, A.F.: Theory of Approximation of Functions of a Real Variable. MacMillan, New York (1963)
Wiener, N.: On the factorization of matrices. Comment. Math. Helv. 29, 97–111 (1955)
Xu, J., Zikatanov, L.: The method of alternating projections and the method of subspace corrections in Hilbert space. J. Amer. Math. Soc. 15, 573–597 (2002)
Acknowledgements
We are grateful to the two referees for raising some points that helped us to make the paper more complete and readable. We are also grateful to Heinz Bauschke who originally pointed out the paper [3] to us that we were unaware of at the time.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2011 Springer Science+Business Media, LLC
About this chapter
Cite this chapter
Deutsch, F., Hundal, H. (2011). Arbitrarily Slow Convergence of Sequences of Linear Operators: A Survey. In: Bauschke, H., Burachik, R., Combettes, P., Elser, V., Luke, D., Wolkowicz, H. (eds) Fixed-Point Algorithms for Inverse Problems in Science and Engineering. Springer Optimization and Its Applications(), vol 49. Springer, New York, NY. https://doi.org/10.1007/978-1-4419-9569-8_11
Download citation
DOI: https://doi.org/10.1007/978-1-4419-9569-8_11
Published:
Publisher Name: Springer, New York, NY
Print ISBN: 978-1-4419-9568-1
Online ISBN: 978-1-4419-9569-8
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)