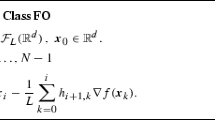Abstract
Let f be a convex function bounded below with infimum f min attained. A bracket is an interval [L, U] containing f min. The Newton Bracketing (NB) method for minimizing f, introduced in [Levin and Ben-Israel, Comput. Optimiz. Appl. 21, 213–229 (2002)], is an iterative method that at each iteration transforms a bracket [L, U] into a strictly smaller bracket \([{L}_{+},{U}_{+}]\) with \(L \leq {L}_{+} < {U}_{+} \leq U\). We show, under certain conditions on f, that a reduction in the bracket ratio \(({U}_{+} - {L}_{+})/(U - L)\) can be guaranteed by the selection of the method parameters.
AMS 2010 Subject Classification: 52A41, 90C25, 49M15, 90B85
This is a preview of subscription content, log in via an institution.
Buying options
Tax calculation will be finalised at checkout
Purchases are for personal use only
Learn about institutional subscriptionsPreview
Unable to display preview. Download preview PDF.
References
Ben-Israel, A., Levin, Y.: The Newton bracketing method for the minimization of convex functions subject to affine constraints. Discrete Appl. Math. 156, 1977–1987 (2008)
Cegielski, A.: A method of projection onto an acute cone with level control in convex minimization. Math. Prog. 85, 469–490 (1999)
Drezner, Z., Klamroth, K., Schöbel, A., Wesolowsky, G.: The Weber problem. In: Z. Dezner, H.W. Hamacher (eds.) Facility Location: Applications and Theory, Springer (2002)
Fortin, C., Wolkowicz, H.: The trust region subproblem and semidefinite programming. Optimization Methods and Software 19, 41–67 (2004)
Held, M., Wolfe, P., Crowder, H.: Validation of subgradient optimization. Math. Prog. 6, 62–88 (1974)
Kim, S., Ahn, H., Cho, S.-C.: Variable target value subgradient method. Math. Prog. 49, 359–369 (1991)
Levin, Y., Ben-Israel, A.: Directional Newton methods in n variables. Math. of Comput. 71, 251–262 (2001)
Levin, Y., Ben-Israel, A.: The Newton bracketing method for convex minimization. Comput. Optimiz. Appl. 21, 213–229 (2002)
Levin, Y., Ben-Israel, A.: A heuristic method for large–scale multifacility location problems. Computers and Operations Research 31, 257–272 (2004)
Love, R.F., Morris, J.G., Wesolowsky, G.O.: Facilities Location: Models and Methods. North-Holland (1988)
Ortega, J.M., Rheinboldt, W.C.: Iterative Solution of Nonlinear Equations in Several Variables. Academic, London (1970)
Ostrwoski, A.M.: Solutions of Equations in Euclidean and Banach Spaces, 3rd edn. Academic (1973)
Poljak, B.T.: Minimization of unsmooth functionals. Z. Vycis. Mat. i Mat. Fiz. 9, 509–521 (1969)
Shor, N.Z.: Application of the Gradient Method for the solution of Network Transportation Problems. Notes, Scientific Seminar on Theory and Application of Cybernetics and Operations Research, Academy of Sciences, Kiev (1962)
Shor, N.Z.: Generalized gradient methods for non-smooth functions and their applications to mathematical programming problems. Ekonomika i Matematicheskie Metody 2, 337–356 (1976)
Shor, N.Z., Kiwiel, K., Ruszcayǹski, A.: Minimization methods for non-differentiable functions. Springer (1985)
Wesolowsky, G.O.: The Weber problem: its history and perspectives. Location Science 1, 5–23 (1993)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2011 Springer Science+Business Media, LLC
About this chapter
Cite this chapter
Ben-Israel, A., Levin, Y. (2011). The Newton Bracketing Method for Convex Minimization: Convergence Analysis. In: Bauschke, H., Burachik, R., Combettes, P., Elser, V., Luke, D., Wolkowicz, H. (eds) Fixed-Point Algorithms for Inverse Problems in Science and Engineering. Springer Optimization and Its Applications(), vol 49. Springer, New York, NY. https://doi.org/10.1007/978-1-4419-9569-8_4
Download citation
DOI: https://doi.org/10.1007/978-1-4419-9569-8_4
Published:
Publisher Name: Springer, New York, NY
Print ISBN: 978-1-4419-9568-1
Online ISBN: 978-1-4419-9569-8
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)