Skip to main content
SpringerLink
Log in

Boundary Control of Korteweg-de Vries and Kuramoto-Sivashinsky PDEs

Encyclopedia of Systems and Control

  • 607 Accesses

Abstract

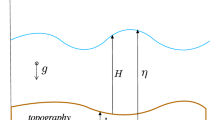
The Korteweg-de Vries (KdV) and the Kuramoto-Sivashinsky (KS) partial differential equations are used to model nonlinear propagation of one-dimensional phenomena. The KdV equation is used in fluid mechanics to describe waves propagation in shallow water surfaces, while the KS equation models front propagation in reaction-diffusion systems. In this article, the boundary control of these equations is considered when they are posed on a bounded interval. Different choices of controls are studied for each equation.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution

Institutional subscriptions

Similar content being viewed by others

Bibliography

  • Armaou A, Christofides PD (2000) Feedback control of the Kuramoto-Sivashinsky equation. Physica D 137:49–61

    Article  MATH  MathSciNet  Google Scholar 

  • Cerpa E (2010) Null controllability and stabilization of a linear Kuramoto-Sivashinsky equation. Commun Pure Appl Anal 9:91–102

    Article  MATH  MathSciNet  Google Scholar 

  • Cerpa E (2013) Control of a Korteweg-de Vries equation: a tutorial. Math Control Rel Fields, accepted

    Google Scholar 

  • Cerpa E, Coron J-M (2013) Rapid stabilization for a Korteweg-de Vries equation from the left dirichlet boundary condition. IEEE Trans Autom Control 58:1688–1695

    Article  MathSciNet  Google Scholar 

  • Cerpa E, Mercado A (2011) Local exact controllability to the trajectories of the 1-D Kuramoto-Sivashinsky equation. J Differ Equ 250:2024–2044

    Article  MATH  MathSciNet  Google Scholar 

  • Cerpa E, Rivas I, Zhang B-Y (2013) Boundary controllability of the Korteweg-de Vries equation on a bounded domain. SIAM J Control Optim, accepted

    Google Scholar 

  • Christofides PD, Armaou A (2000) Global stabilization of the Kuramoto-Sivashinsky equation via distributed output feedback control. Syst Control Lett 39:283–294

    Article  MATH  MathSciNet  Google Scholar 

  • Coron JM (2007) Control and nonlinearity. American Mathematical Society, Providence

    MATH  Google Scholar 

  • Coron J-M, Crépeau E (2004) Exact boundary controllability of a nonlinear KdV equation with critical lengths. J Eur Math Soc 6:367–398

    Article  MATH  Google Scholar 

  • Glass O, Guerrero S (2008) Some exact controllability results for the linear KdV equation and uniform controllability in the zero-dispersion limit. Asymptot Anal 60:61–100

    MATH  MathSciNet  Google Scholar 

  • Glass O, Guerrero S (2010) Controllability of the KdV equation from the right Dirichlet boundary condition. Syst Control Lett 59:390–395

    Article  MATH  MathSciNet  Google Scholar 

  • Korteweg DJ, de Vries G (1895) On the change of form of long waves advancing in a rectangular canal, and on a new type of long stationary waves. Philos Mag 39:422–443

    Article  MATH  Google Scholar 

  • Krstic M (2009) Delay compensation for nonlinear, adaptive, and PDE systems. Birkhauser, Boston

    Book  MATH  Google Scholar 

  • Kuramoto Y, Tsuzuki T (1975) On the formation of dissipative structures in reaction-diffusion systems. Theor Phys 54:687–699

    Article  Google Scholar 

  • Lin Guo Y-J (2002) Null boundary controllability for a fourth order parabolic equation. Taiwan J Math 6:421–431

    MATH  Google Scholar 

  • Liu W-J, Krstic M (2001) Stability enhancement by boundary control in the Kuramoto-Sivashinsky equation. Nonlinear Anal Ser A Theory Methods 43:485–507

    Article  MATH  MathSciNet  Google Scholar 

  • Perla Menzala G, Vasconcellos CF, Zuazua E (2002) Stabilization of the Korteweg-de Vries equation with localized damping. Q Appl Math LX:111–129

    Google Scholar 

  • Rosier L (1997) Exact boundary controllability for the Korteweg-de Vries equation on a bounded domain. ESAIM Control Optim Calc Var 2:33–55

    Article  MATH  MathSciNet  Google Scholar 

  • Rosier L, Zhang B-Y (2009) Control and stabilization of the Korteweg-de Vries equation: recent progresses. J Syst Sci Complex 22:647–682

    Article  MathSciNet  Google Scholar 

  • Sivashinsky GI (1977) Nonlinear analysis of hydrodynamic instability in laminar flames – I derivation of basic equations. Acta Astronaut 4:1177–1206

    Article  MATH  MathSciNet  Google Scholar 

  • Smyshlyaev A, Krstic M (2010) Adaptive control of parabolic PDEs. Princeton University Press, Princeton

    MATH  Google Scholar 

  • Zhang BY (1999) Exact boundary controllability of the Korteweg-de Vries equation. SIAM J Control Optim 37:543–565

    Article  MATH  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Departamento de Matemática, Universidad Técnica Federico Santa María, Avda. España 1680, Valparaiso, Chile

    Eduardo Cerpa

Authors
  1. Eduardo Cerpa
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Eduardo Cerpa .

Editor information

Editors and Affiliations

  1. Electrical and Computer Engineering, Boston University, Boston, Massachusetts, USA

    John Baillieul

  2. Automation and Control Solutions, Honeywell, Golden Valley, Minnesota, USA

    Tariq Samad

Rights and permissions

Reprints and permissions

Copyright information

© 2013 Springer-Verlag London

About this entry

Cite this entry

Cerpa, E. (2013). Boundary Control of Korteweg-de Vries and Kuramoto-Sivashinsky PDEs. In: Baillieul, J., Samad, T. (eds) Encyclopedia of Systems and Control. Springer, London. https://doi.org/10.1007/978-1-4471-5102-9_13-1

Download citation

  • DOI: https://doi.org/10.1007/978-1-4471-5102-9_13-1

  • Received:

  • Accepted:

  • Published:

  • Publisher Name: Springer, London

  • Online ISBN: 978-1-4471-5102-9

  • eBook Packages: Springer Reference EngineeringReference Module Computer Science and Engineering

Publish with us

Policies and ethics

Chapter history

  1. Latest

    Boundary Control of Korteweg-de Vries and Kuramoto-Sivashinsky PDEs
    Published:
    07 November 2019

    DOI: https://doi.org/10.1007/978-1-4471-5102-9_13-2

  2. Original

    Boundary Control of Korteweg-de Vries and Kuramoto-Sivashinsky PDEs
    Published:
    15 March 2014

    DOI: https://doi.org/10.1007/978-1-4471-5102-9_13-1

Search

Navigation