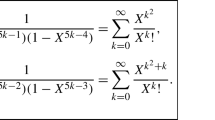Overview
- Authors:
-
-
Arto Salomaa
-
Department of Mathematics, University of Turku, Turku 50, Finland
-
Matti Soittola
-
Department of Mathematics, University of Turku, Turku 50, Finland
Access this book
Other ways to access
About this book
This book develops a theory of formal power series in noncommuting variables, the main emphasis being on results applicable to automata and formal language theory. This theory was initiated around 196O-apart from some scattered work done earlier in connection with free groups-by M. P. Schutzenberger to whom also belong some of the main results. So far there is no book in existence concerning this theory. This lack has had the unfortunate effect that formal power series have not been known and used by theoretical computer scientists to the extent they in our estimation should have been. As with most mathematical formalisms, the formalism of power series is capable of unifying and generalizing known results. However, it is also capable of establishing specific results which are difficult if not impossible to establish by other means. This is a point we hope to be able to make in this book. That formal power series constitute a powerful tool in automata and language theory depends on the fact that they in a sense lead to the arithmetization of automata and language theory. We invite the reader to prove, for instance, Theorem IV. 5. 3 or Corollaries III. 7. 8 and III. 7.- all specific results in language theory-by some other means. Although this book is mostly self-contained, the reader is assumed to have some background in algebra and analysis, as well as in automata and formal language theory.
Similar content being viewed by others
Article
Open access
18 August 2022
Article
29 September 2021
Table of contents (4 chapters)
-
-
- Arto Salomaa, Matti Soittola
Pages 1-15
-
- Arto Salomaa, Matti Soittola
Pages 16-75
-
- Arto Salomaa, Matti Soittola
Pages 76-117
-
- Arto Salomaa, Matti Soittola
Pages 118-162
-
Back Matter
Pages 163-174