Abstract
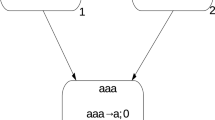
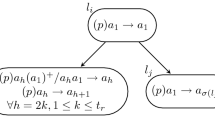
We present the known results pertaining to the recently introduced spiking neural P Systems with communication on request (SNQ P Systems). Aside from showing the properties of these systems working with multiple types of spikes (as defined originally) we also give the results obtained by our group in the area of SNQ P Systems using only one type of spikes. All the results are given from the perspective of descriptional complexity, taking into account the number of neurons needed in the universal systems. Several open problems and ideas for improvements of the results are also presented.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
References
Bîlbîe, F.-D., Păun, A.: Universality of SNQ P systems using one type of spikes. In: Proceedings of the 18th International Conference on Membrane Computing (CMC 2017), Bradford, UK, 25–28 July 2017
Carbarle, F.G.C., Adorna, H.N., Pérez-Jiménez, M.J.: Sequential spiking neural P systems with structural plasticity based on max/min spike number. Neural Comput. Appl. 27(5), 1337–1347 (2016)
Chen, H., Freund, R., Ionescu, M., Păun, G., Pérez-Jiménez, M.J.: On string languages generated by spiking neural P systems. Fundam. Inform. 18(6), 1371–1382 (2007)
Csuhaj-Varju, E.: Grammar Systems: A Grammatical Approach to Distribution and Cooperation. Gordon and Breach, London (1994)
Ibarra, O.H., Păun, A., Rodríguez-Patón, A.: Sequential SNP systems based on min/max spike number. Theor. Comput. Sci. 410, 2982–2991 (2009)
Ionescu, M., Păun, G., Yokomori, T.: Spiking neural P systems. Fundam. Inform. 71(2–3), 279–308 (2006)
Ionescu, M., Păun, A., Păun, G., Pérez-Jiménez, M.J.: Computing with spiking neural P systems: traces and small universal systems. In: Mao, C., Yokomori, T. (eds.) DNA 2006. LNCS, vol. 4287, pp. 1–16. Springer, Heidelberg (2006). https://doi.org/10.1007/11925903_1
Korec, I.: Small universal register machines. Theor. Comput. Sci. 168, 267–301 (1996)
Leporati, A., Mauri, G., Zandron, C., Păun, G., Pérez-Jiménez, M.J.: Uniform solutions to SAT and Subset Sum by spiking neural P systems. Nat. Comput. 8(4), 681–702 (2009)
Minsky, M.: Computation - Finite and Infinite Machines. Prentice Hall, Englewood Cliffs (1967)
Pan, L., Păun, G., Zhang, G., Neri, F.: Spiking neural P systems with communication on request. Int. J. Neural Syst. 28(08), 1750042 (2017)
Pan, L., Păun, G., Pérez-Jiménez, M.J.: Spiking neural P systems with neuron division and budding. Sci. China Inf. Sci. 54(8), 1596–1607 (2011)
Pan, T., Shi, X., Zhang, Z., Xu, F.: A small universal spiking neural P system with communication on request. Neurocomputing 275, 1622–1628 (2018)
Păun, A., Bîlbîe, F.-D.: Universality of SNQ P systems using one type of spikes and restrictive rule application. Int. J. Comput. Sci. (2018, accepted)
Păun, G.: Membrane Computing - An Introduction. Springer, Berlin (2002). https://doi.org/10.1007/978-3-642-56196-2
Păun, G.: Grammar systems: a grammatical approach to distribution and cooperation. In: Fülöp, Z., Gécseg, F. (eds.) ICALP 1995. LNCS, vol. 944, pp. 429–443. Springer, Heidelberg (1995). https://doi.org/10.1007/3-540-60084-1_94
Păun, G., Pérez-Jiménez, M.J., Rozenberg, G.: Computing morphisms by spiking neural P systems. Int. J. Comput. Sci. 18(6), 1371–1382 (2007)
Păun, G., Pérez-Jiménez, M.J., Rozenberg, G.: Spike trains in spiking neural P systems. Int. J. Found. Comput. Sci. 17(04), 975–1002 (2006)
Rozenberg, G., Salomaa, A. (eds.): Handbook of Formal Languages, vol. 3. Springer, Berlin (1997). https://doi.org/10.1007/978-3-642-59126-6
Schroeppel, R.: A two counter machine cannot calculate \(2^N\). Technical report AIM-257, A. I. Laboratory, Massachusetts Institute of Technology, Cambridge, MA, 1–31 May 1972. ftp://publications.ai.mit.edu/ai-publications/pdf/AIM-257.pdf. Accessed 14 Oct 2015
Wang, J., Hoogeboom, H.J., Pan, L., Păun, G., Pérez-Jiménez, M.J.: Spiking neural P systems with weights. Neural Comput. 22(10), 1615–2646 (2010)
Wu, T., Bîlbîe, F.-D., Păun, A., Pan, L., Neri, F.: Simplified and yet Turing universal spiking neural P systems with communication on request. Int. J. Neural Syst. (2018, accepted)
Zhang, G., Rong, H., Neri, F., Pérez-Jiménez, M.J.: An optimization spiking neural P system for approximately solving combinatorial optimization problems. Int. J. Neural Syst. 24(5), 1440006 (2014)
Zeng, X., Pan, L., Pérez-Jiménez, M.J.: Small universal simple spiking neural P systems with weights. Sci. China Inf. Sci. 57(9), 1–11 (2014)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 Springer Nature Switzerland AG
About this chapter
Cite this chapter
Păun, A., Bîlbîe, FD. (2018). A Look at the Descriptional Complexity of SNQ P Systems. In: Graciani, C., Riscos-Núñez, A., Păun, G., Rozenberg, G., Salomaa, A. (eds) Enjoying Natural Computing. Lecture Notes in Computer Science(), vol 11270. Springer, Cham. https://doi.org/10.1007/978-3-030-00265-7_18
Download citation
DOI: https://doi.org/10.1007/978-3-030-00265-7_18
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-00264-0
Online ISBN: 978-3-030-00265-7
eBook Packages: Computer ScienceComputer Science (R0)