1 Introduction

Recently, deep convolution neural networks (CNNs) have shown excellent performance on various computer vision and medical image analysis tasks including semantic segmentation [1]. Early CNN approaches use sliding windows and approach segmentation as many independent classifications, which is inefficient. Fully-convolutional networks (FCN) [2] instead directly operate on full images. Consequentially, FCNs are more efficient and many FCN variants achieve state-of-the-art segmentation performance [3, 4]. When dealing with 3D image segmentations, the simplest approach is to treat a 3D volume as a sequence of 2D slices [5] and to segment them independently with a 2D CNN. However, this overlooks correlations across slices. To account for such correlations while avoiding 3D CNNs, triplanar schemes [6] have been proposed which apply 2D CNNs on image slices from three orthogonal planes of an image volume. Naturally, applying a 3D CNN to an image volume can take advantage of the full 3D information, but has high computational cost and memory requirements.

Most existing work on semantic segmentation focuses on improving performance by designing deeper and more complex networks. This, generally results in better performance, but comes at the cost of additional complexity, especially for the segmentation of 3D images. Hence, it would be beneficial to design more efficient network architectures for 3D segmentation while retaining segmentation performance. Inspired by work that applies an auto-context approach [7] to CNN models [8] and additive learning schemes such as boosting [9], we propose a cascaded 3D semantic segmentation framework composed of a sequence of 3D FCNs with contextual inputs and additive outputs. As an alternative design strategy to a monolithic complex deep FCN, we show that such a sequence of simpler and shallower FCNs achieves performance on par with a more complex network, but using two orders of magnitude less parameters. This approach also allows to trade-off model accuracy with run-time and memory requirements.

Contributions: (1) We show that a cascaded model composed of several simple FCNs can perform as well as a single complex FCN with almost two orders of magnitude more parameters, resulting in better computational efficiency. (2) Our additive model shows better performance than an auto-context approach using contextual input (i.e., segmentations) only without the additive strategy. (3) We provide an analysis to give insight into why the additive output helps refine the segmentation model. (4) Lastly, we evaluate our model on a relatively large knee MRI dataset from the Osteoarthritis Initiative for cartilage segmentation.

2 Methods

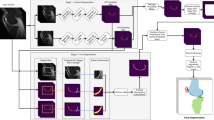
In this section we (1) introduce the two components of our cascaded framework: contextual input and additive output; (2) provide an analysis illuminating the effect of additive outputs; and (3) describe the FCNs used to construct the cascaded models in our experiments. Figure 1 illustrates the proposed approach.

Fig. 1.
figure 1

Schematic diagram of proposed contextual additive model.

Full size image

2.1 Contextual Additive Networks

Context information is useful for image segmentation [7, 10]. Inspired by the auto-context algorithm [7], cascaded models have been proposed that input the concatenation of an image and a segmentation (either the resulting labeling itself or the class label probabilities) to subsequent models. The segmentation is generated by a previous model with the image as its only input. Furthermore, residual skip connections [11] are widely used for CNNs. These help the training of deep networks and boost performance. Our contextual additive network is inspired by both approaches. However, instead of using the residual connections across layers inside a neural network, we use them to connect the output of each sub-model to generate the class probability. We use a sequence of such models each also having access to the original input image (see Fig. 1).

Formally, our cascaded model \(\mathbf {\Phi }\) is based on a sequence of FCNs \(\{\phi ^0, \phi ^1, ..., \phi ^M\}\), whose parameters are \(\mathbf {\Theta } = \{\varvec{\theta }^0, \varvec{\theta }^1, ..., \varvec{\theta }^M\}\) respectively. The first FCN, \(\phi ^0\), with parameters \(\varvec{\theta }^0\) takes an image x as input and predicts the probability map of all class labels, \(P^0\), by applying softmax to the output of the FCN: \(P^0(x;\varvec{\theta }^0) = \sigma (\phi ^0(x;\varvec{\theta }^0))\), where \(\sigma \) is the softmax function. For an output \(z\in \mathbb {R}^{C}\) of C classes, the probability of class j is

$$\begin{aligned} \sigma (z)_j = \frac{e^{z_j}}{\sum _{l=0}^{C-1}e^{z_l}},~c\in \{0,\cdots ,C-1\}. \end{aligned}$$
(1)

Subsequent FCNs use the image and the probability map (i.e., the contextual input) of the previous FCN as input. However, instead of directly predicting the input to a softmax function to obtain label probabilities these subsequent FCNs (unlike previous work [8]) predict a residual between the previous prediction, added to the output of the previous stage (i.e., the additive output) before the softmax. The output of the contextual additive model after the M-th FCN is

$$\begin{aligned} P^M (x;\mathbf {\Theta })= \sigma (\phi ^0(x;\varvec{\theta }^0) + \sum _{m=1}^{M}\phi ^m(x, P^{m-1}; \varvec{\theta }^m)). \end{aligned}$$
(2)

Such a cascaded model can be trained by training each additive FCN via:

$$\begin{aligned} \hat{\varvec{\theta }}^m = \mathop {\text {arg min }}\limits _{\varvec{\theta }^m} \mathcal {L}(Y, P^m(X;\{\hat{\varvec{\theta }}^0, \cdots , \hat{\varvec{\theta }}^{m-1},\varvec{\theta }^m\})), \end{aligned}$$
(3)

where Y denotes the set of label images, X the set of images in the training dataset, and \(\mathcal {L}\) is the chosen loss function. Alternatively it can be trained end-to-end by minimizing the sum of the losses for all stages of the model:

$$\begin{aligned} \hat{\mathbf {\Theta }}= \{\hat{\varvec{\theta }}^0, \hat{\varvec{\theta }}^1, ..., \hat{\varvec{\theta }}^M\} = \mathop {\text {arg min}}\limits _{\mathbf {\Theta }} \sum _{m=0}^{M}\mathcal {L}(Y, P^m(X;\{\varvec{\theta }^0, ..., \varvec{\theta }^m\})). \end{aligned}$$
(4)

Both training strategies work well in our experiments. When applying the trained model one obtains the class label by selecting the most probable label:

$$\begin{aligned} \hat{y}(x;\hat{\mathbf {\Theta }}) = \mathop {\text {arg max }}\limits _j P_j^M(x;\hat{\mathbf {\Theta }}), \end{aligned}$$
(5)

where \(\hat{y}\) denotes the label output for input image x and model parameters \(\hat{\mathbf {\Theta }}\).

2.2 Why an Additive Network is Beneficial

To give insight into the effect of adding model outputs before the softmax in the cascade we approximate the loss function to first order. We use the cross-entropy loss for multi-class segmentation which for a single model output, \(\phi ^0\), is

$$\begin{aligned} \mathcal {L}_{CE}^0 = - \sum _{j=0}^{C-1}y_j \ln (\sigma (\phi ^0_j)), \end{aligned}$$
(6)

where j is the class index and C is the total number of classes. Considering a cascaded model of two FCNs, we assume we trained the first FCN \(\phi ^0\) by optimizing \(\mathcal {L}_{CE}^0\). With the additive output of the second model, the loss becomes

$$\begin{aligned} \mathcal {L}_{CE}^1 = - \sum _{j=0}^{C-1}y_j \ln (\sigma (\phi ^0+\phi ^1)_j). \end{aligned}$$
(7)

We can think of \(\phi ^1\) as a perturbation to \(\phi ^0\). Approximating the loss function (7) around \(\phi ^0\) via a Taylor series expansion results in

$$\begin{aligned} \mathcal {L}_{CE}^1&\approx - \sum _{j=0}^{C-1}y_j \ln (\sigma (\phi ^0_j)) - \sum _{j=0}^{C-1}y_j \sum _{l=0}^{C-1} \frac{\partial \ln \sigma (\phi ^0)_j}{\partial \phi ^0_l}\phi ^1_l \nonumber \\&= \mathcal {L}_{CE}^0 +\sum _{j=0}^{C-1}y_j \sum _{l=0}^{C-1} \varDelta {\mathcal {L}_{CE}^1}_j(\phi ^1_l|\phi ^0), \end{aligned}$$
(8)

where \(\mathcal {L}_{CE}^0\) only depends on \(\phi ^0\) and can therefore be ignored for sequential training of \(\phi ^1\); \(\varDelta {\mathcal {L}_{CE}^1}_j(\phi ^1_l|\phi ^0)\) captures how the loss depends on the output of the second model for class l, \(\phi ^1_l\), for voxels annotated as class j:

$$\begin{aligned} \varDelta {\mathcal {L}_{CE}^1}_j(\phi ^1_l|\phi ^0) = \left\{ \begin{array}{lr} -(1-\sigma (\phi ^0_j))\phi ^1_j = -(1-P_j^0)\phi _j^1 &{} , \; l = j\\ \sigma (\phi ^0_l)\phi ^1_l = P_l^0\phi _l^1 &{} , \; l \ne j \end{array} \right. . \end{aligned}$$
(9)

Intuitively, when the first model performs well \(P^0_j\) is high and \(P^0_{l, l\ne j}\) is low; increasing \(\phi ^1_j\) and decreasing \(\phi ^1_{l, l\ne j}\) is of low benefit to reduce the loss. When the first model performs badly \(P^0_j\) is low and \(P^0_{l, l\ne j}\) is high; increasing \(\phi ^1_j\) and decreasing \(\phi ^1_{l, l\ne j}\) is of high benefit. I.e., improving the prediction where the first model perform badly is more beneficial than improving already good predictions. In effect, the loss of the additive model naturally weighs each voxel so that it focuses on problematic regions.

2.3 3D Fully Convolution Networks

Many FCN variants exist [3, 12]. The U-Net [13] and the 3D U-Net [14] have been popular to segment medical images. U-Nets add skip connections between the encoder/decoder paths to retain high resolution features. We use the 3D U-Net as our elementary FCN because of its good performance. The original 3D U-Net is a dense architecture with four resolution steps in the encoder/decoder paths, and 512 feature channels at the bottleneck, resulting in a total of \(\sim \)19 million parameters. We also build three simpler U-Nets with fewer feature channels and fewer resolution levels (Fig. 2). The smallest one has only 45,808 parameters.

Fig. 2.
figure 2

U-Nets of the cascaded models (# of parameters in parentheses): original U-Net (\(\sim \)19M), U-Net-1 (\(\sim \)1.1M), U-Net-2 (\(\sim \)287K), U-Net-3 (\(\sim \)46K)

Full size image

3 Experiments

For each U-Net, we train a cascaded model of length M, where M is larger for smaller U-Nets as the performance of a model with more complex U-Nets saturates with smaller M. We explore results for end-to-end and sequential training. We also use only contextual input and only additive output for our cascaded U-Net-3\(\,\times \,\)6 model to investigate the impact of our two key techniques. We study memory use and runtime to explore our model’s segmentation efficiency.

3.1 Dataset and Preprocessing

We use knee MRIs from the Osteoarthritis Initiative consisting of 176 MR images from 88 patients (2 longitudinal scans per patient). We split the dataset into a training set of 60 patients (120 images), a validation set of 8 patients (16 images) and a test set of 20 patients (40 images). All images are of size \(384\,\times \,384\,\times \,160\) and resolution \(0.36\,\times \,0.36\,\times \,0.7\,\mathrm{mm}^3\) per voxel. We normalize the intensities of each image such that the 0.1 percentile and the 99.9 percentile are mapped to \(\{0,1\}\) and clamp values that are smaller to 0 and larger to 1 to avoid outliers. We did not apply bias-field correction, because our exploratory experiments indicated that bias-field correction did not substantially impact segmentation results. For each volume, femoral and tibial cartilage are annotated on sagittal slices. We transform the corresponding 2D polygon annotations to 3D label maps.

Table 1. Models’ parameter size and memory consumption in sequential training
Full size table

3.2 Implementation Details

Due to the high memory demands of 3D convolutions, the full image volume and its network outputs may not fit on a single GPU. Hence, we use overlapping tiles as in the U-Net [13]. We choose image patches of size \(128\,\times \,128\,\times \,32\) considering the nonuniform voxel resolution and that annotations were drawn sagittally.

During training, we randomly crop 3D patch pairs from image-label pairs. To avoid class imbalances due to the high proportion of background voxels we use three types of patches: any possible patch, patches with more than \(r_1\%\) of femoral cartilage voxels, and patches with more that \(r_2\%\) tibial cartilage voxels. Patches are randomly sampled at a ratio of 1 : 1 : 2 (\(r_1 = 1\), \(r_2 = 2\)). We use the Adam [15] optimizer with first moment \(\beta _1=0.9\), second moment \(\beta _2=0.999\), and \(\epsilon =1e{-}10\). The learning rate is initialized as \(5e{-}4\) and decays at half of the total epochs and at the beginning of the last 50 epochs by 0.2. We train the original U-Net and each sub-network in the sequentially trained cascaded models with 600 epochs. When training a cascaded model of M U-Nets end-to-end, \(100*(M-1)\) extra epochs were applied to assure convergence. Regarding training time, the cascaded models take less time than the original U-Net (13 h) except U-Net-3\(\,\times \,\)6 (17 h for end-to-end training and 20 h for sequential training). During training, we recorded a model’s Dice score on the validation dataset and evaluate the model with the best validation score on the separate testing dataset.

Table 2. Segmentation evaluation of contextual additive models using different U-Nets. E.g. U-Net-1\(\,\times \,2\) is a cascaded model of two U-Net-1. Results are for sequential training (end-to-end results in parentheses). Our models can achieve performance on par with the original U-Net with much fewer parameters and lower memory requirements.
Full size table

4 Results and Discussion

We quantitatively evaluate the segmentation results of each model and the output at intermediate stages. Table 2 shows average Dice scores (DSC) and the mean Intersection of Union (mIOU) of femoral and tibial cartilage and their standard deviations. We also report the performance of U-Net-3\(\,\times \,6\) models using contextual input or additive output only. The number of model parameters and memory consumption in sequential training (batch size 4) and testing (batch size 8) are given in Table 1. Table 3 shows segmentation results at different stages of the U-Net-3\(\,\times \,6\) cascade.

We observe that our contextual additive networks are more efficient as they use significantly fewer parameters while achieving similar or better performance than using a single more complex U-Net. The original U-Net has for example almost two orders of magnitude more parameters than the U-Net-3\(\,\times \,\)6 while resulting in very similar accuracy. We also observe that both the contextual inputs and the additive output helps boost the performance in cascaded U-Nets.

Table 3. Segmentation results of end-to-end trained U-Net-3\(\,\times \,\)6. Rows are Sagittal, Axial, Coronal views and 3D rendering. Red and green labels represent femoral and tibial cartilage respectively.
Full size table

5 Conclusion

We developed a framework of cascaded FCNs with contextual inputs and additive output to boost the performance of 3D semantic segmentation. Our theoretical analysis shows that the additive output focuses the additive model on regions where previous output results were relatively poor. Experiments on a large 3D MRI knee dataset demonstrated that our framework can refine the results of a single U-Net. Importantly, we showed that a cascaded model of simple U-Nets can match the performance of a complex U-Net, while providing better efficiency in terms of using fewer parameters and requiring less memory. Our approach may provide an alternative to improve FCNs for segmentation. Future work will investigate different FCNs as elements of the cascade, e.g. networks with inputs of multiple resolutions, and evaluate performance on different datasets.