Abstract
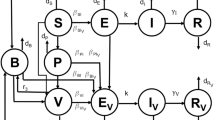
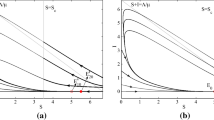
This paper relies on a minimum-time vaccination control strategy for a class of epidemic models. A targeted state final value is defined as a certain accuracy closed ball around some point being a reasonable approximate measure of both disease- free equilibrium points associated with the two vaccination levels used for the optimal- time control.
This is a preview of subscription content, log in via an institution to check access.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
References
De la Sen, M., Alonso-Quesada, S.: Control issues for the beverton-holt equation in ecology by locally monitoring the environment carrying capacity: non-adaptive and adaptive cases. Appl. Math. Comput. 215, 2616–2633 (2009)
De la Sen, M., Alonso-Quesada, S.: Model-matching bases control of the bevertoon-holt equation in ecology. Discrete Dyn. Nat. Soc. (2008). Article number 793512
De la Sen, M.: Fundamental properties of linear control systems with after-effect-I. The continuous case. Math. Comput. Model. 10, 473–489 (1988)
De la Sen, M.: The generalized beverton-holt equation and the control of populations. Appl. Math. Model. 32, 2312–2328 (2008)
De la Sen, M., Ibeas, A., Alonso-Quesada, S., Nistal, R.: On a new epidemic model with asymptomatic and dead-infective subpopulations with feedback controls useful for Ebola disease. Discrete Dyn. Nat. Soc. (2017). Article number 4232971
Karnik, A., Dayama, P.: Optimal control of information epidemics. In: 2012 Fourth International Conference on Communications Systems and Networks (COMSNETS) (2012). 1
Workman, M.L., Kosut, R.L., Franklin, G.F.: Adaptive proximate time- optimal servomechanisms. Discrete-time case. In: Proceedings of the American Control Conference, pp. 1548–1553 (2002). 1
Kim, S., Choi, D.S.: Time-optimal control of state-constrained second-order systems and an application to robotic manipulators. In: Proceedings of the American Control Conference, pp. 1478–1483 (2002). 1
You, K.I., Lee, E.B.: Robust near time-optimal control of nonlinear second-order systems with model uncertainty. In: Proceedings of the IEEE International Conference on Control Applications, pp. 232–236 (2000). 1
Keeling, M.J., Rohani, P.: Modeling Infectious Diseases in Humans and Animals. Princeton University Press, Princeton and Oxford (2008)
Acknowledgments
This research has been supported by the Spanish Government and by the European Fund of Regional Development FEDER through Grant DPI2015-64766-R (MINECO/FEDER, UE) and by UPV/EHU by Grant PGC 17/33.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this paper
Cite this paper
De la Sen, M., Ibeas, A., Alonso-Quesada, S., Nistal, R. (2019). A Strategy for Minimum Time Equilibrium Targetting in Epidemic Diseases. In: Vasant, P., Zelinka, I., Weber, GW. (eds) Intelligent Computing & Optimization. ICO 2018. Advances in Intelligent Systems and Computing, vol 866. Springer, Cham. https://doi.org/10.1007/978-3-030-00979-3_40
Download citation
DOI: https://doi.org/10.1007/978-3-030-00979-3_40
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-00978-6
Online ISBN: 978-3-030-00979-3
eBook Packages: EngineeringEngineering (R0)